Fuzzy Clustering to Identify Clusters at Different Levels of Fuzziness: An Evolutionary Multi-Objective Optimization Approach
Paper and Code
Aug 09, 2018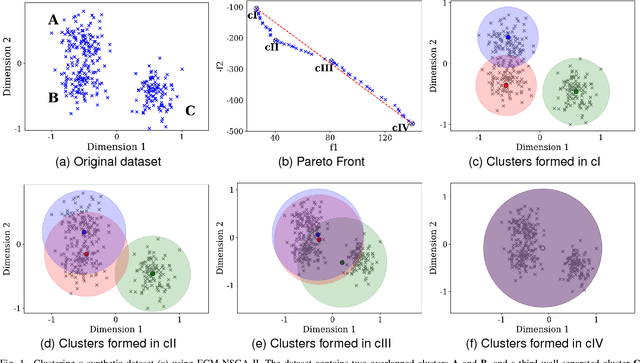
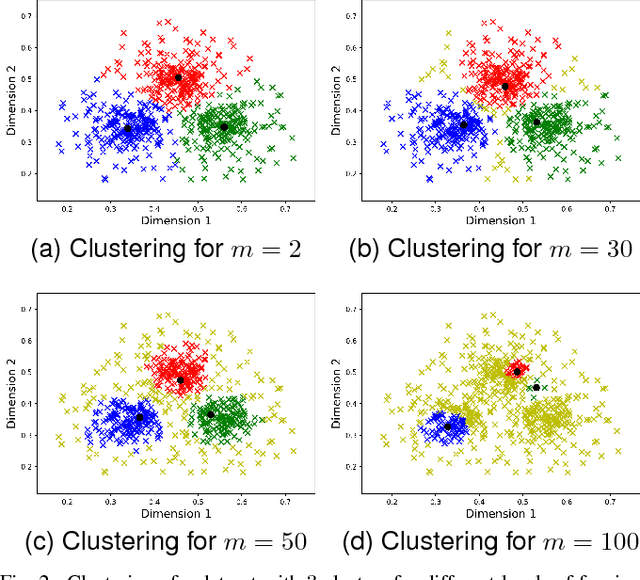
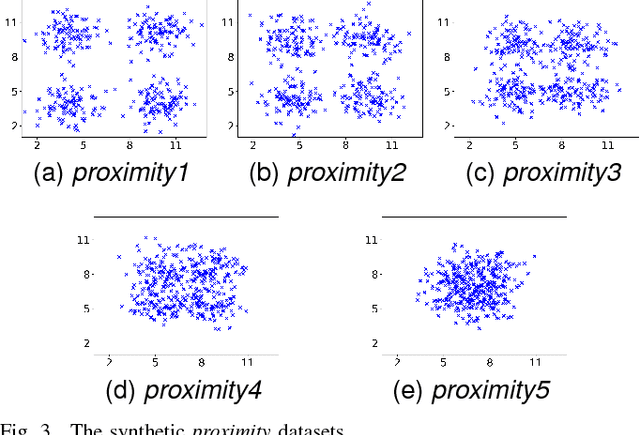
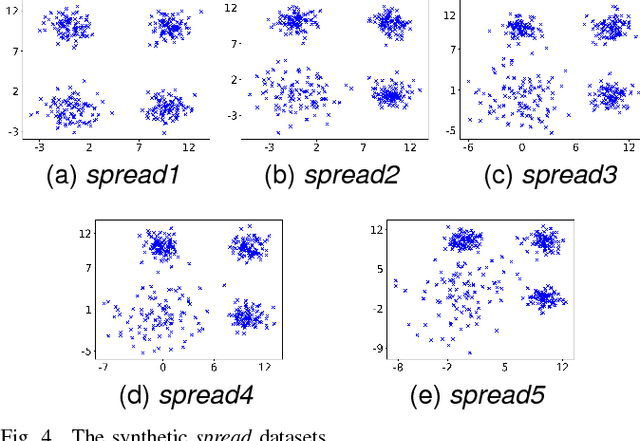
Fuzzy clustering methods identify naturally occurring clusters in a dataset, where the extent to which different clusters are overlapped can differ. Most methods have a parameter to fix the level of fuzziness. However, the appropriate level of fuzziness depends on the application at hand. This paper presents Entropy $c$-Means (ECM), a method of fuzzy clustering that simultaneously optimizes two contradictory objective functions, resulting in the creation of fuzzy clusters with different levels of fuzziness. This allows ECM to identify clusters with different degrees of overlap. ECM optimizes the two objective functions using two multi-objective optimization methods, Non-dominated Sorting Genetic Algorithm II (NSGA-II), and Multiobjective Evolutionary Algorithm based on Decomposition (MOEA/D). We also propose a method to select a suitable trade-off clustering from the Pareto front. Experiments on challenging synthetic datasets as well as real-world datasets show that ECM leads to better cluster detection compared to the conventional fuzzy clustering methods as well as previously used multi-objective methods for fuzzy clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge