FuSSO: Functional Shrinkage and Selection Operator
Paper and Code
Mar 09, 2014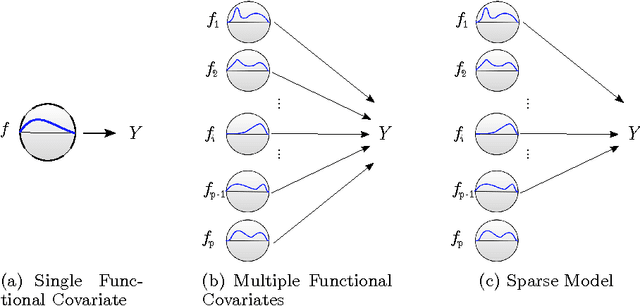
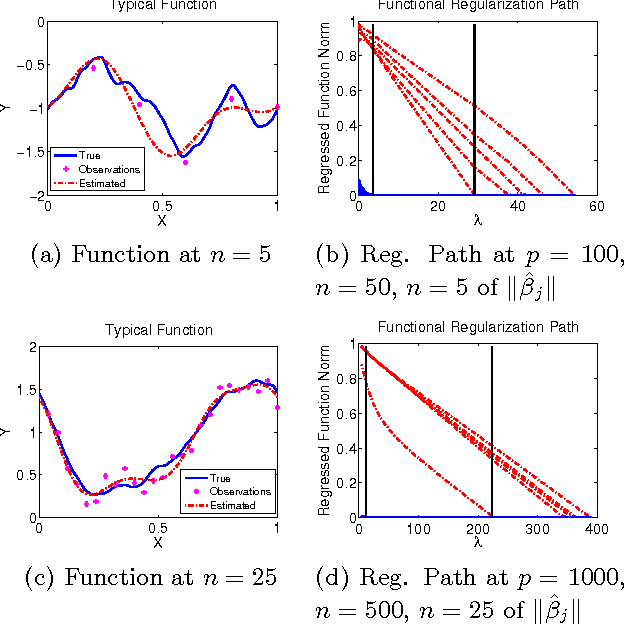
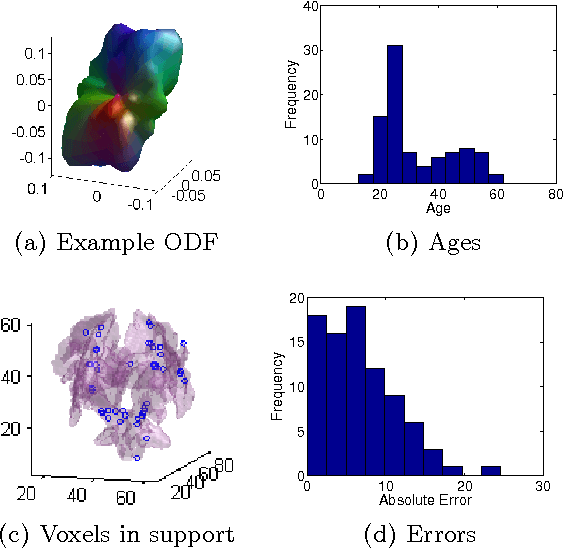
We present the FuSSO, a functional analogue to the LASSO, that efficiently finds a sparse set of functional input covariates to regress a real-valued response against. The FuSSO does so in a semi-parametric fashion, making no parametric assumptions about the nature of input functional covariates and assuming a linear form to the mapping of functional covariates to the response. We provide a statistical backing for use of the FuSSO via proof of asymptotic sparsistency under various conditions. Furthermore, we observe good results on both synthetic and real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge