Formulating Robustness Against Unforeseen Attacks

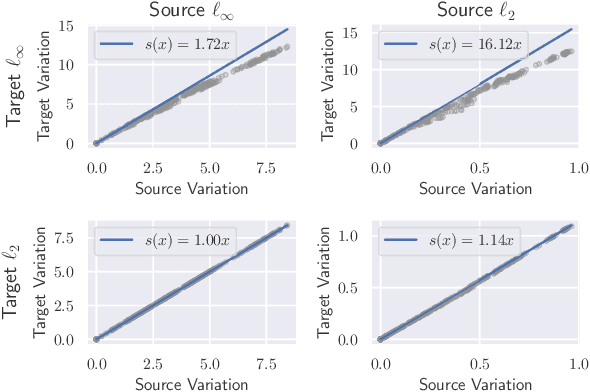
Existing defenses against adversarial examples such as adversarial training typically assume that the adversary will conform to a specific or known threat model, such as $\ell_p$ perturbations within a fixed budget. In this paper, we focus on the scenario where there is a mismatch in the threat model assumed by the defense during training, and the actual capabilities of the adversary at test time. We ask the question: if the learner trains against a specific "source" threat model, when can we expect robustness to generalize to a stronger unknown "target" threat model during test-time? Our key contribution is to formally define the problem of learning and generalization with an unforeseen adversary, which helps us reason about the increase in adversarial risk from the conventional perspective of a known adversary. Applying our framework, we derive a generalization bound which relates the generalization gap between source and target threat models to variation of the feature extractor, which measures the expected maximum difference between extracted features across a given threat model. Based on our generalization bound, we propose adversarial training with variation regularization (AT-VR) which reduces variation of the feature extractor across the source threat model during training. We empirically demonstrate that AT-VR can lead to improved generalization to unforeseen attacks during test-time compared to standard adversarial training on Gaussian and image datasets.