For interpolating kernel machines, the minimum norm ERM solution is the most stable
Paper and Code
Jun 28, 2020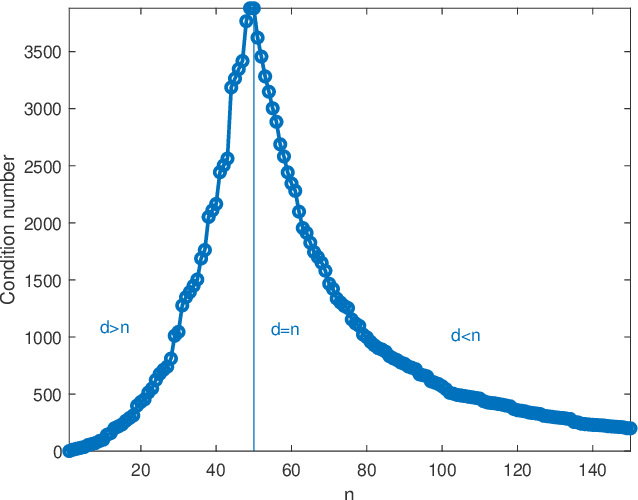
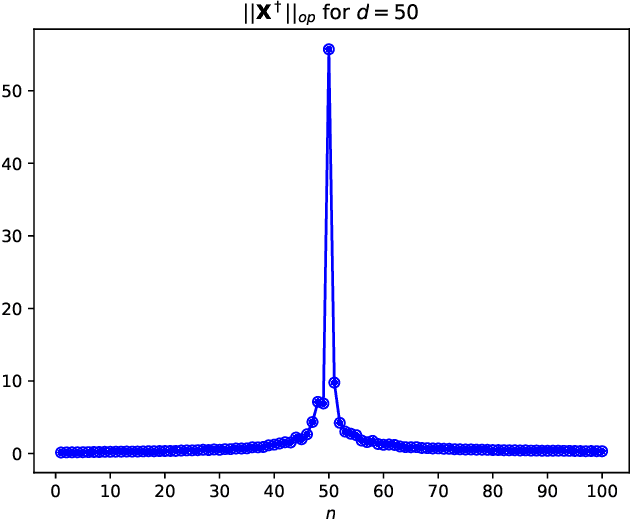
We study the average $\mbox{CV}_{loo}$ stability of kernel ridge-less regression and derive corresponding risk bounds. We show that the interpolating solution with minimum norm has the best $\mbox{CV}_{loo}$ stability, which in turn is controlled by the condition number of the empirical kernel matrix. The latter can be characterized in the asymptotic regime where both the dimension and cardinality of the data go to infinity. Under the assumption of random kernel matrices, the corresponding test error follows a double descent curve.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge