Fisher-Pitman permutation tests based on nonparametric Poisson mixtures with application to single cell genomics
Paper and Code
Jun 06, 2021
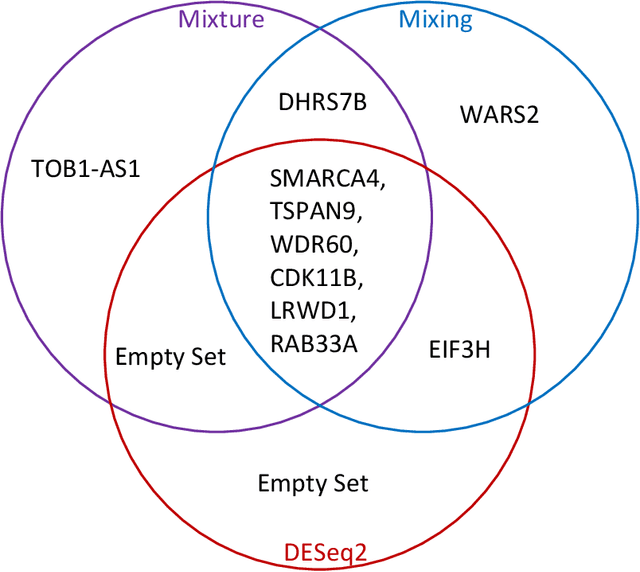
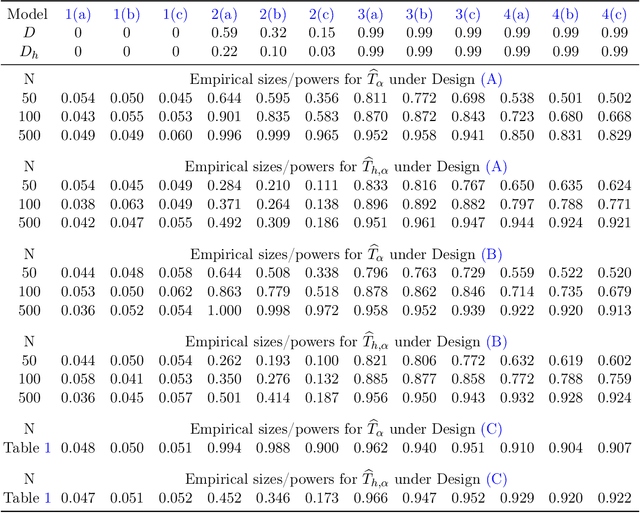
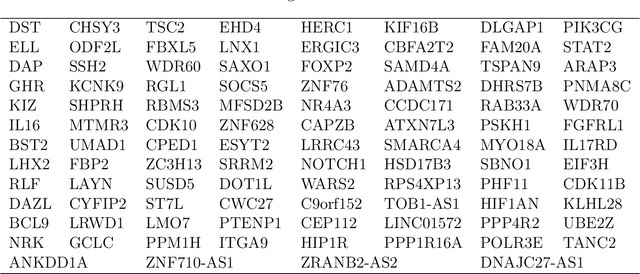
This paper investigates the theoretical and empirical performance of Fisher-Pitman-type permutation tests for assessing the equality of unknown Poisson mixture distributions. Building on nonparametric maximum likelihood estimators (NPMLEs) of the mixing distribution, these tests are theoretically shown to be able to adapt to complicated unspecified structures of count data and also consistent against their corresponding ANOVA-type alternatives; the latter is a result in parallel to classic claims made by Robinson (Robinson, 1973). The studied methods are then applied to a single-cell RNA-seq data obtained from different cell types from brain samples of autism subjects and healthy controls; empirically, they unveil genes that are differentially expressed between autism and control subjects yet are missed using common tests. For justifying their use, rate optimality of NPMLEs is also established in settings similar to nonparametric Gaussian (Wu and Yang, 2020a) and binomial mixtures (Tian et al., 2017; Vinayak et al., 2019).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge