Fermion Sampling Made More Efficient
Paper and Code
Sep 15, 2021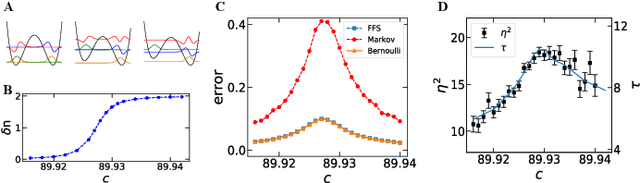
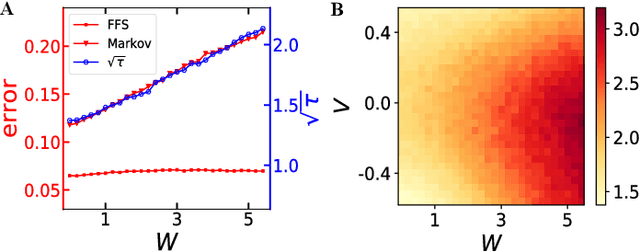
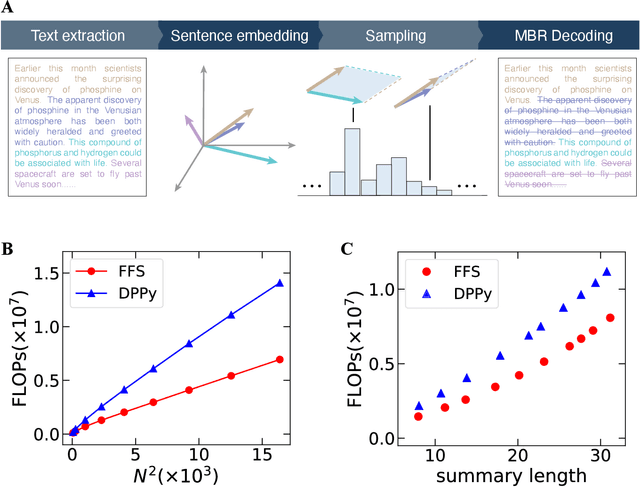
Fermion sampling is to generate probability distribution of a many-body Slater-determinant wavefunction, which is termed "determinantal point process" in statistical analysis. For its inherently-embedded Pauli exclusion principle, its application reaches beyond simulating fermionic quantum many-body physics to constructing machine learning models for diversified datasets. Here we propose a fermion sampling algorithm, which has a polynomial time-complexity -- quadratic in the fermion number and linear in the system size. This algorithm is about 100% more efficient in computation time than the best known algorithms. In sampling the corresponding marginal distribution, our algorithm has a more drastic improvement, achieving a scaling advantage. We demonstrate its power on several test applications, including sampling fermions in a many-body system and a machine learning task of text summarization, and confirm its improved computation efficiency over other methods by counting floating-point operations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge