FedUV: Uniformity and Variance for Heterogeneous Federated Learning
Paper and Code
Mar 01, 2024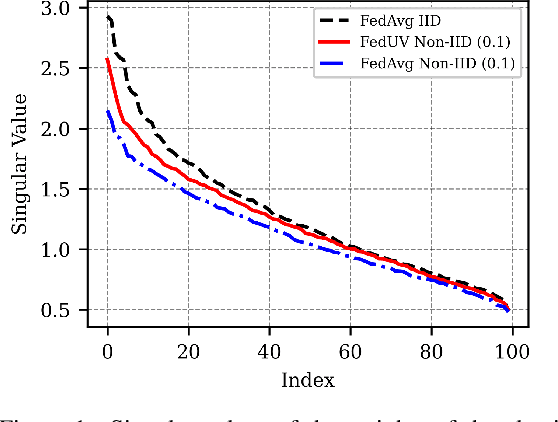

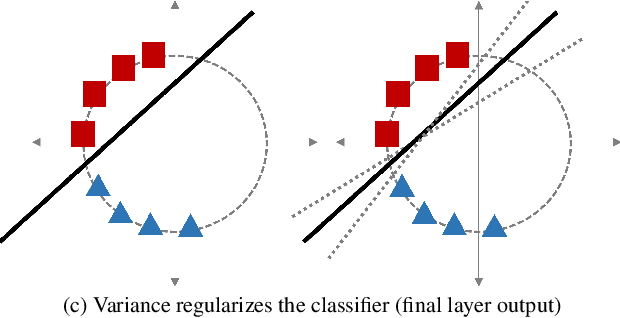

Federated learning is a promising framework to train neural networks with widely distributed data. However, performance degrades heavily with heterogeneously distributed data. Recent work has shown this is due to the final layer of the network being most prone to local bias, some finding success freezing the final layer as an orthogonal classifier. We investigate the training dynamics of the classifier by applying SVD to the weights motivated by the observation that freezing weights results in constant singular values. We find that there are differences when training in IID and non-IID settings. Based on this finding, we introduce two regularization terms for local training to continuously emulate IID settings: (1) variance in the dimension-wise probability distribution of the classifier and (2) hyperspherical uniformity of representations of the encoder. These regularizations promote local models to act as if it were in an IID setting regardless of the local data distribution, thus offsetting proneness to bias while being flexible to the data. On extensive experiments in both label-shift and feature-shift settings, we verify that our method achieves highest performance by a large margin especially in highly non-IID cases in addition to being scalable to larger models and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge