FedLGA: Towards System-Heterogeneity of Federated Learning via Local Gradient Approximation
Paper and Code
Dec 22, 2021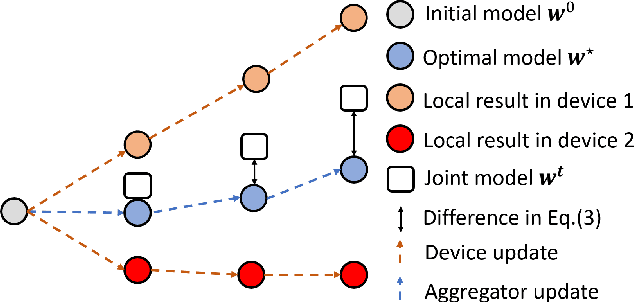
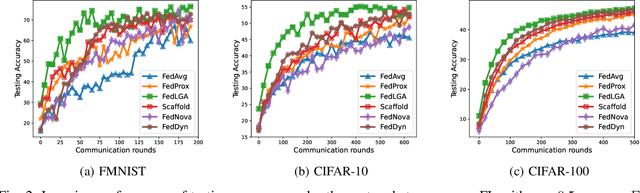
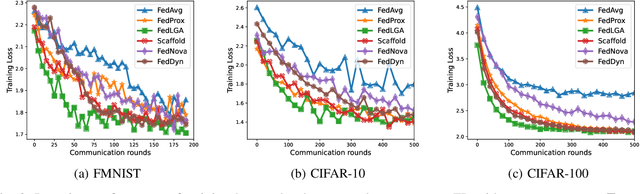
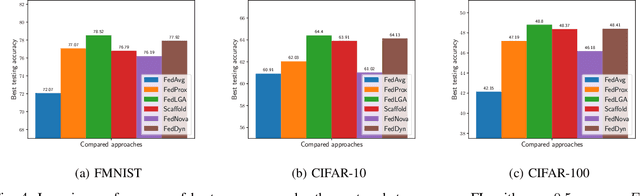
Federated Learning (FL) is a decentralized machine learning architecture, which leverages a large number of remote devices to learn a joint model with distributed training data. However, the system-heterogeneity is one major challenge in a FL network to achieve robust distributed learning performance, which is of two aspects: i) device-heterogeneity due to the diverse computational capacity among devices; ii) data-heterogeneity due to the non-identically distributed data across the network. Though there have been benchmarks against the heterogeneous FL, e.g., FedProx, the prior studies lack formalization and it remains an open problem. In this work, we formalize the system-heterogeneous FL problem and propose a new algorithm, called FedLGA, which addresses this problem by bridging the divergence of local model updates via gradient approximation. To achieve this, FedLGA provides an alternated Hessian estimation method, which only requires extra linear complexity on the aggregator. Theoretically, we show that with a device-heterogeneous ratio $\rho$, FedLGA achieves convergence rates on non-i.i.d distributed FL training data against non-convex optimization problems for $\mathcal{O} \left( \frac{(1+\rho)}{\sqrt{ENT}} + \frac{1}{T} \right)$ and $\mathcal{O} \left( \frac{(1+\rho)\sqrt{E}}{\sqrt{TK}} + \frac{1}{T} \right)$ for full and partial device participation respectively, where $E$ is the number of local learning epoch, $T$ is the number of total communication round, $N$ is the total device number and $K$ is the number of selected device in one communication round under partially participation scheme. The results of comprehensive experiments on multiple datasets show that FedLGA outperforms current FL benchmarks against the system-heterogeneity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge