Federated LQR: Learning through Sharing
Paper and Code
Nov 03, 2020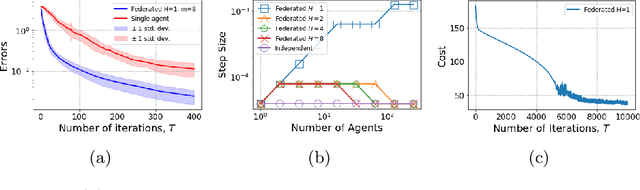
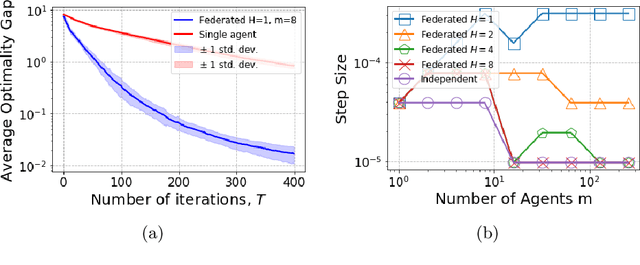
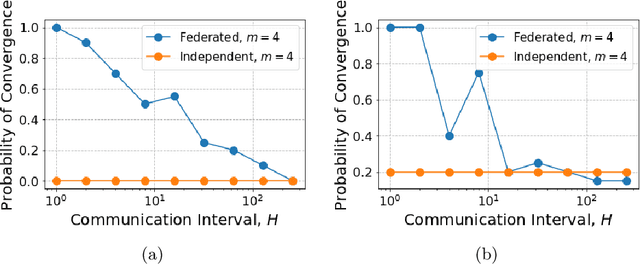
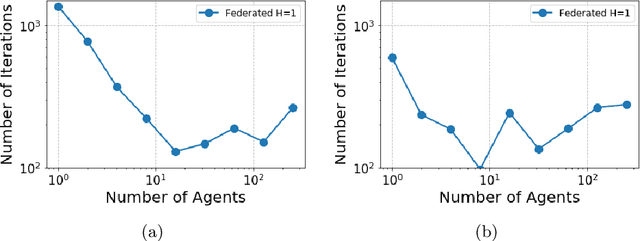
In many multi-agent reinforcement learning applications such as flocking, multi-robot applications and smart manufacturing, distinct agents share similar dynamics but face different objectives. In these applications, an important question is how the similarities amongst the agents can accelerate learning in spite of the agents' differing goals. We study a distributed LQR (Linear Quadratic Regulator) tracking problem which models this setting, where the agents, acting independently, share identical (unknown) dynamics and cost structure but need to track different targets. In this paper, we propose a communication-efficient, federated model-free zeroth-order algorithm that provably achieves a convergence speedup linear in the number of agents compared with the communication-free setup where each agent's problem is treated independently. We support our arguments with numerical simulations of both linear and nonlinear systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge