Federated Learning via Posterior Averaging: A New Perspective and Practical Algorithms
Paper and Code
Oct 11, 2020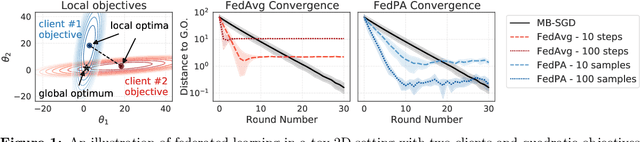

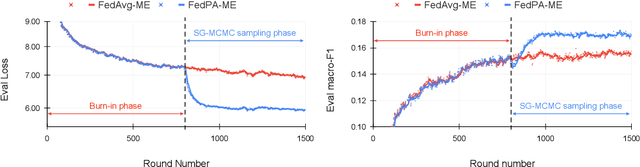

Federated learning is typically approached as an optimization problem, where the goal is to minimize a global loss function by distributing computation across client devices that possess local data and specify different parts of the global objective. We present an alternative perspective and formulate federated learning as a posterior inference problem, where the goal is to infer a global posterior distribution by having client devices each infer the posterior of their local data. While exact inference is often intractable, this perspective provides a principled way to search for global optima in federated settings. Further, starting with the analysis of federated quadratic objectives, we develop a computation- and communication-efficient approximate posterior inference algorithm -- federated posterior averaging (FedPA). Our algorithm uses MCMC for approximate inference of local posteriors on the clients and efficiently communicates their statistics to the server, where the latter uses them to refine a global estimate of the posterior mode. Finally, we show that FedPA generalizes federated averaging (FedAvg), can similarly benefit from adaptive optimizers, and yields state-of-the-art results on four realistic and challenging benchmarks, converging faster, to better optima.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge