FedAvg with Fine Tuning: Local Updates Lead to Representation Learning
Paper and Code
May 27, 2022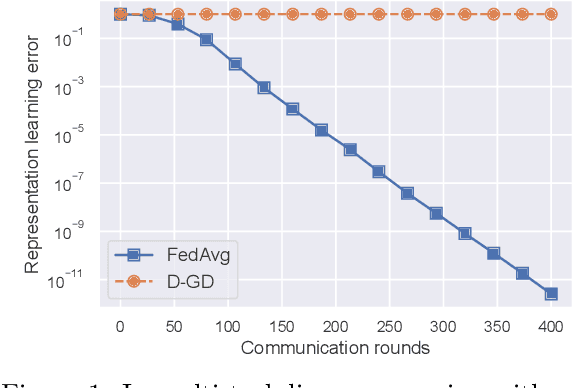


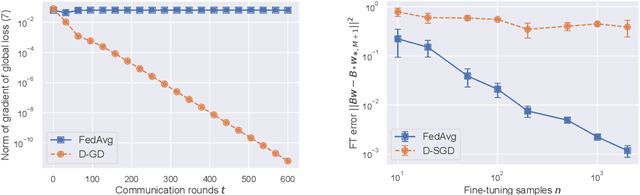
The Federated Averaging (FedAvg) algorithm, which consists of alternating between a few local stochastic gradient updates at client nodes, followed by a model averaging update at the server, is perhaps the most commonly used method in Federated Learning. Notwithstanding its simplicity, several empirical studies have illustrated that the output model of FedAvg, after a few fine-tuning steps, leads to a model that generalizes well to new unseen tasks. This surprising performance of such a simple method, however, is not fully understood from a theoretical point of view. In this paper, we formally investigate this phenomenon in the multi-task linear representation setting. We show that the reason behind generalizability of the FedAvg's output is its power in learning the common data representation among the clients' tasks, by leveraging the diversity among client data distributions via local updates. We formally establish the iteration complexity required by the clients for proving such result in the setting where the underlying shared representation is a linear map. To the best of our knowledge, this is the first such result for any setting. We also provide empirical evidence demonstrating FedAvg's representation learning ability in federated image classification with heterogeneous data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge