Fed-ZOE: Communication-Efficient Over-the-Air Federated Learning via Zeroth-Order Estimation
Paper and Code
Dec 21, 2024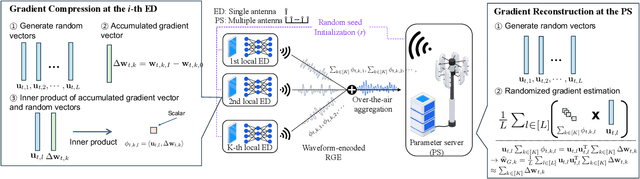
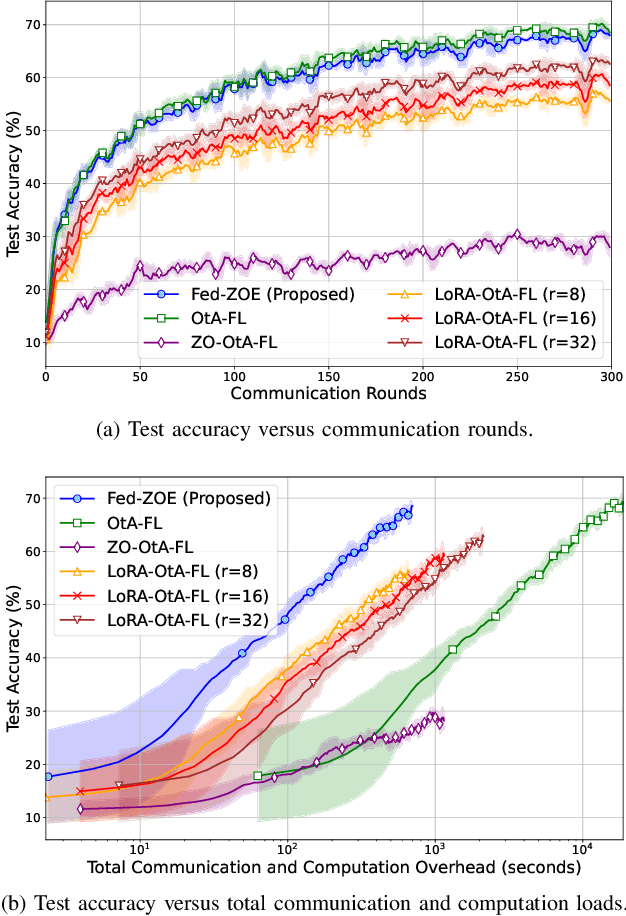

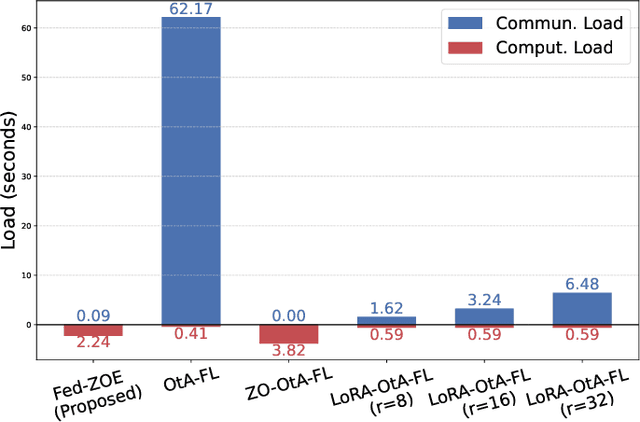
As 6G and beyond networks grow increasingly complex and interconnected, federated learning (FL) emerges as an indispensable paradigm for securely and efficiently leveraging decentralized edge data for AI. By virtue of the superposition property of communication signals, over-the-air FL (OtA-FL) achieves constant communication overhead irrespective of the number of edge devices (EDs). However, training neural networks over the air still incurs substantial communication costs, as the number of transmitted symbols equals the number of trainable parameters. To alleviate this issue, the most straightforward approach is to reduce the number of transmitted symbols by 1) gradient compression and 2) gradient sparsification. Unfortunately, these methods are incompatible with OtA-FL due to the loss of its superposition property. In this work, we introduce federated zeroth-order estimation (Fed-ZOE), an efficient framework inspired by the randomized gradient estimator (RGE) commonly used in zeroth-order optimization (ZOO). In FedZOE, EDs perform local weight updates as in standard FL, but instead of transmitting full gradient vectors, they send compressed local model update vectors in the form of several scalar-valued inner products between the local model update vectors and random vectors. These scalar values enable the parameter server (PS) to reconstruct the gradient using the RGE trick with highly reduced overhead, as well as preserving the superposition property. Unlike conventional ZOO leveraging RGE for step-wise gradient descent, Fed-ZOE compresses local model update vectors before transmission, thereby achieving higher accuracy and computational efficiency. Numerical evaluations using ResNet-18 on datasets such as CIFAR-10, TinyImageNet, SVHN, CIFAR-100, and Brain-CT demonstrate that Fed-ZOE achieves performance comparable to Fed-OtA while drastically reducing communication costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge