FeatureNorm: L2 Feature Normalization for Dynamic Graph Embedding
Paper and Code
Feb 27, 2021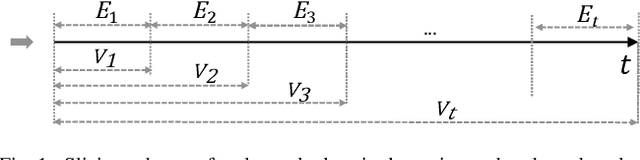
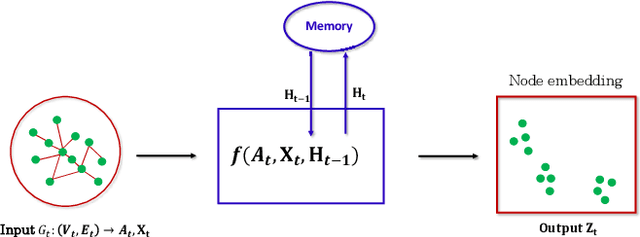
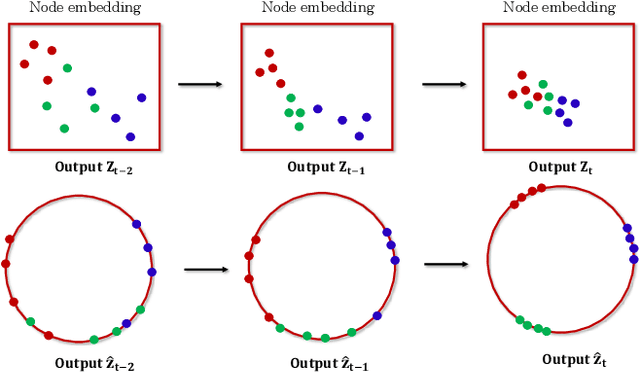
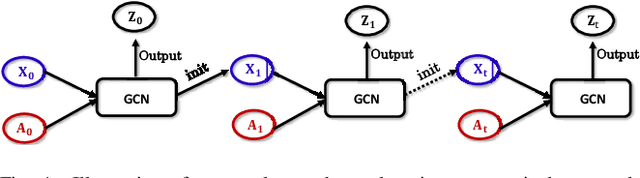
Dynamic graphs arise in a plethora of practical scenarios such as social networks, communication networks, and financial transaction networks. Given a dynamic graph, it is fundamental and essential to learn a graph representation that is expected not only to preserve structural proximity but also jointly capture the time-evolving patterns. Recently, graph convolutional network (GCN) has been widely explored and used in non-Euclidean application domains. The main success of GCN, especially in handling dependencies and passing messages within nodes, lies in its approximation to Laplacian smoothing. As a matter of fact, this smoothing technique can not only encourage must-link node pairs to get closer but also push cannot-link pairs to shrink together, which potentially cause serious feature shrink or oversmoothing problem, especially when stacking graph convolution in multiple layers or steps. For learning time-evolving patterns, a natural solution is to preserve historical state and combine it with the current interactions to obtain the most recent representation. Then the serious feature shrink or oversmoothing problem could happen when stacking graph convolution explicitly or implicitly according to current prevalent methods, which would make nodes too similar to distinguish each other. To solve this problem in dynamic graph embedding, we analyze the shrinking properties in the node embedding space at first, and then design a simple yet versatile method, which exploits L2 feature normalization constraint to rescale all nodes to hypersphere of a unit ball so that nodes would not shrink together, and yet similar nodes can still get closer. Extensive experiments on four real-world dynamic graph datasets compared with competitive baseline models demonstrate the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge