FastSurvival: Hidden Computational Blessings in Training Cox Proportional Hazards Models
Paper and Code
Oct 24, 2024
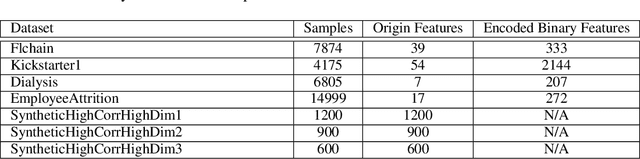
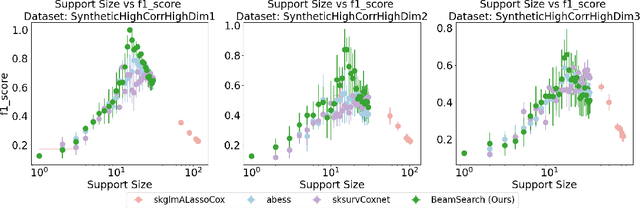
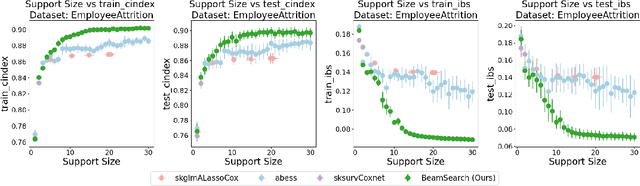
Survival analysis is an important research topic with applications in healthcare, business, and manufacturing. One essential tool in this area is the Cox proportional hazards (CPH) model, which is widely used for its interpretability, flexibility, and predictive performance. However, for modern data science challenges such as high dimensionality (both $n$ and $p$) and high feature correlations, current algorithms to train the CPH model have drawbacks, preventing us from using the CPH model at its full potential. The root cause is that the current algorithms, based on the Newton method, have trouble converging due to vanishing second order derivatives when outside the local region of the minimizer. To circumvent this problem, we propose new optimization methods by constructing and minimizing surrogate functions that exploit hidden mathematical structures of the CPH model. Our new methods are easy to implement and ensure monotonic loss decrease and global convergence. Empirically, we verify the computational efficiency of our methods. As a direct application, we show how our optimization methods can be used to solve the cardinality-constrained CPH problem, producing very sparse high-quality models that were not previously practical to construct. We list several extensions that our breakthrough enables, including optimization opportunities, theoretical questions on CPH's mathematical structure, as well as other CPH-related applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge