FastAdaBelief: Improving Convergence Rate for Belief-based Adaptive Optimizer by Strong Convexity
Paper and Code
Apr 28, 2021

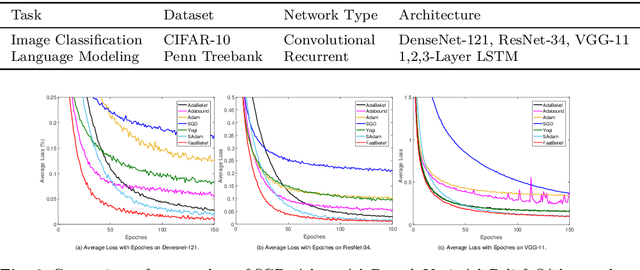
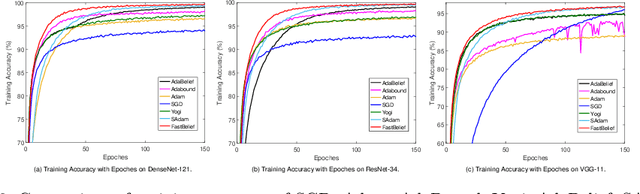
The AdaBelief algorithm demonstrates superior generalization ability to the Adam algorithm by viewing the exponential moving average of observed gradients. AdaBelief is proved to have a data-dependent $O(\sqrt{T})$ regret bound when objective functions are convex, where $T$ is a time horizon. However, it remains to be an open problem on how to exploit strong convexity to further improve the convergence rate of AdaBelief. To tackle this problem, we present a novel optimization algorithm under strong convexity, called FastAdaBelief. We prove that FastAdaBelief attains a data-dependant $O(\log T)$ regret bound, which is substantially lower than AdaBelief. In addition, the theoretical analysis is validated by extensive experiments performed on open datasets (i.e., CIFAR-10 and Penn Treebank) for image classification and language modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge