Fast Variational Block-Sparse Bayesian Learning

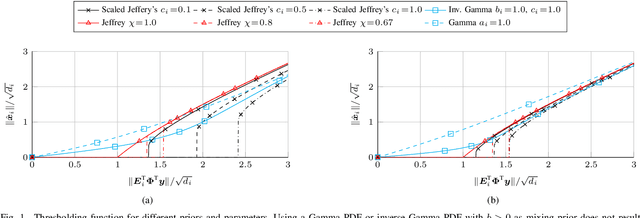
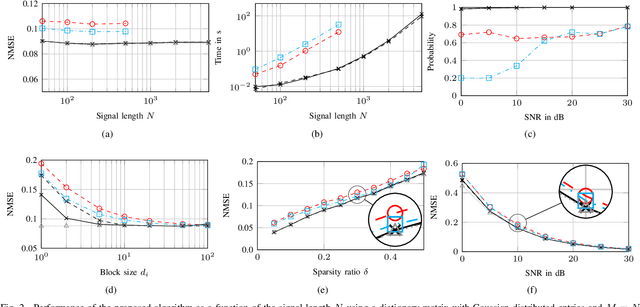
We present a fast update rule for variational block-sparse Bayesian learning (SBL) methods. Using a variational Bayesian framework, we show how repeated updates of probability density functions (PDFs) of the prior variances and weights can be expressed as a nonlinear first-order recurrence from one estimate of the parameters of the proxy PDFs to the next. Specifically, the recurrent relation turns out to be a strictly increasing rational function for many commonly used prior PDFs of the variances, such as Jeffrey's prior. Hence, the fixed points of this recurrent relation can be obtained by solving for the roots of a polynomial. This scheme allows to check for convergence/divergence of individual prior variances in a single step. Thereby, the the computational complexity of the variational block-SBL algorithm is reduced and the convergence speed is improved by two orders of magnitude in our simulations. Furthermore, the solution allows insights into the sparsity of the estimators obtained by choosing different priors.