Fast Threshold Tests for Detecting Discrimination
Paper and Code
Mar 10, 2018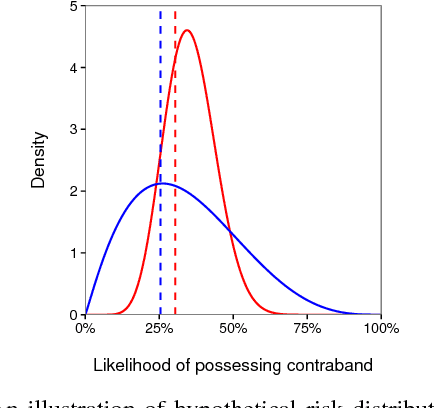

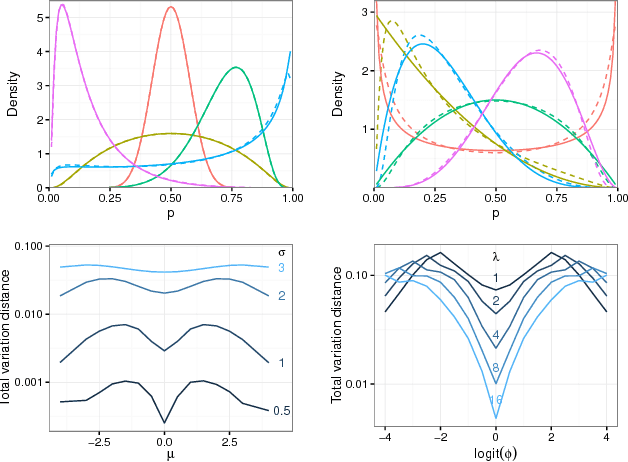
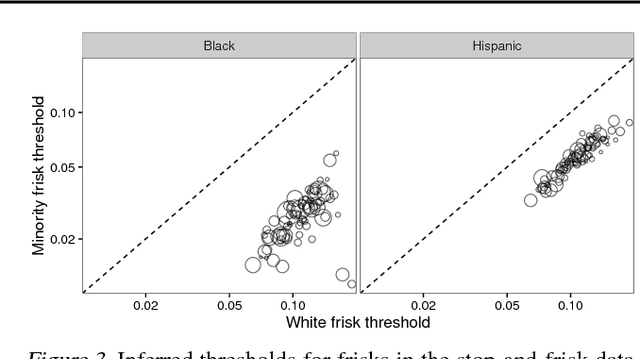
Threshold tests have recently been proposed as a useful method for detecting bias in lending, hiring, and policing decisions. For example, in the case of credit extensions, these tests aim to estimate the bar for granting loans to white and minority applicants, with a higher inferred threshold for minorities indicative of discrimination. This technique, however, requires fitting a complex Bayesian latent variable model for which inference is often computationally challenging. Here we develop a method for fitting threshold tests that is two orders of magnitude faster than the existing approach, reducing computation from hours to minutes. To achieve these performance gains, we introduce and analyze a flexible family of probability distributions on the interval [0, 1] -- which we call discriminant distributions -- that is computationally efficient to work with. We demonstrate our technique by analyzing 2.7 million police stops of pedestrians in New York City.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge