Fast Randomized Semi-Supervised Clustering
Paper and Code
Oct 09, 2016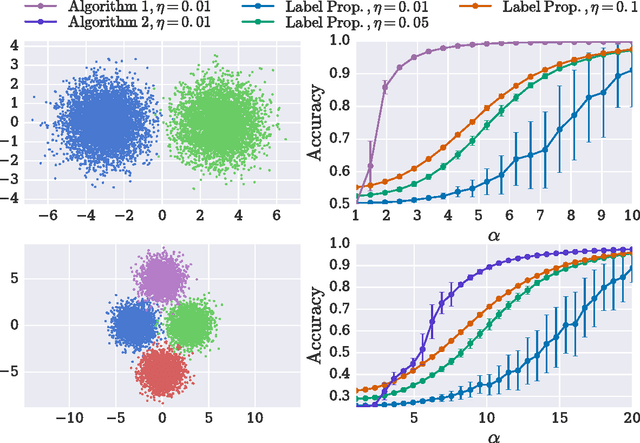
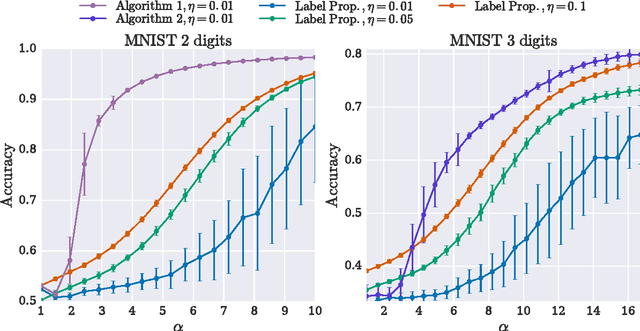
We consider the problem of clustering partially labeled data from a minimal number of randomly chosen pairwise comparisons between the items. We introduce an efficient local algorithm based on a power iteration of the non-backtracking operator and study its performance on a simple model. For the case of two clusters, we give bounds on the classification error and show that a small error can be achieved from $O(n)$ randomly chosen measurements, where $n$ is the number of items in the dataset. Our algorithm is therefore efficient both in terms of time and space complexities. We also investigate numerically the performance of the algorithm on synthetic and real world data.
* Journal of Physics: Conf. Series 1036 (2018) 012015
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge