Fast Parallel SVM using Data Augmentation
Paper and Code
Dec 24, 2015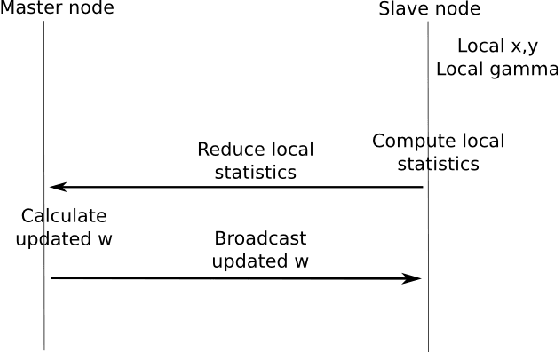
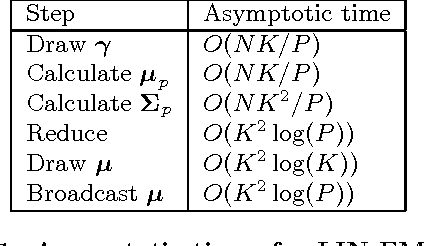

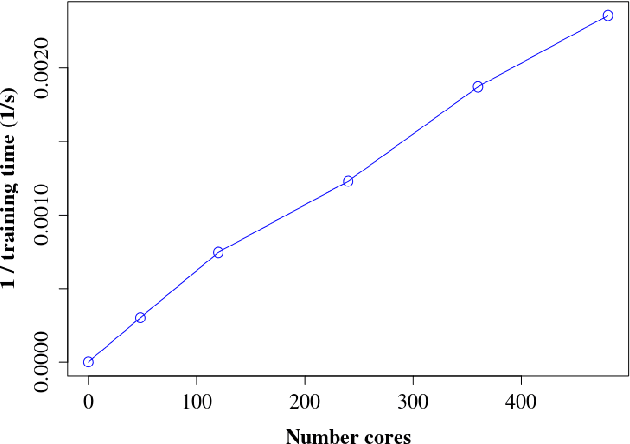
As one of the most popular classifiers, linear SVMs still have challenges in dealing with very large-scale problems, even though linear or sub-linear algorithms have been developed recently on single machines. Parallel computing methods have been developed for learning large-scale SVMs. However, existing methods rely on solving local sub-optimization problems. In this paper, we develop a novel parallel algorithm for learning large-scale linear SVM. Our approach is based on a data augmentation equivalent formulation, which casts the problem of learning SVM as a Bayesian inference problem, for which we can develop very efficient parallel sampling methods. We provide empirical results for this parallel sampling SVM, and provide extensions for SVR, non-linear kernels, and provide a parallel implementation of the Crammer and Singer model. This approach is very promising in its own right, and further is a very useful technique to parallelize a broader family of general maximum-margin models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge