Fast online ranking with fairness of exposure
Paper and Code
Sep 13, 2022
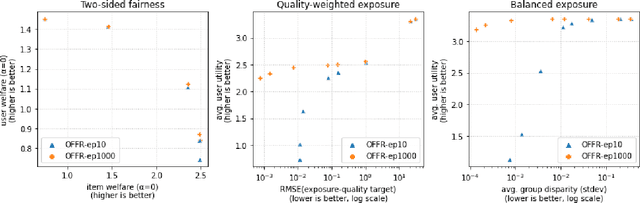
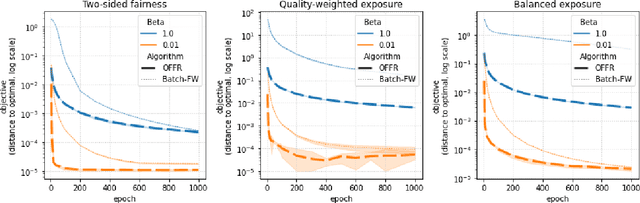
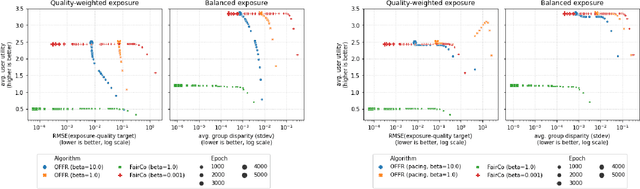
As recommender systems become increasingly central for sorting and prioritizing the content available online, they have a growing impact on the opportunities or revenue of their items producers. For instance, they influence which recruiter a resume is recommended to, or to whom and how much a music track, video or news article is being exposed. This calls for recommendation approaches that not only maximize (a proxy of) user satisfaction, but also consider some notion of fairness in the exposure of items or groups of items. Formally, such recommendations are usually obtained by maximizing a concave objective function in the space of randomized rankings. When the total exposure of an item is defined as the sum of its exposure over users, the optimal rankings of every users become coupled, which makes the optimization process challenging. Existing approaches to find these rankings either solve the global optimization problem in a batch setting, i.e., for all users at once, which makes them inapplicable at scale, or are based on heuristics that have weak theoretical guarantees. In this paper, we propose the first efficient online algorithm to optimize concave objective functions in the space of rankings which applies to every concave and smooth objective function, such as the ones found for fairness of exposure. Based on online variants of the Frank-Wolfe algorithm, we show that our algorithm is computationally fast, generating rankings on-the-fly with computation cost dominated by the sort operation, memory efficient, and has strong theoretical guarantees. Compared to baseline policies that only maximize user-side performance, our algorithm allows to incorporate complex fairness of exposure criteria in the recommendations with negligible computational overhead.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge