Faith-Shap: The Faithful Shapley Interaction Index
Paper and Code
Mar 09, 2022
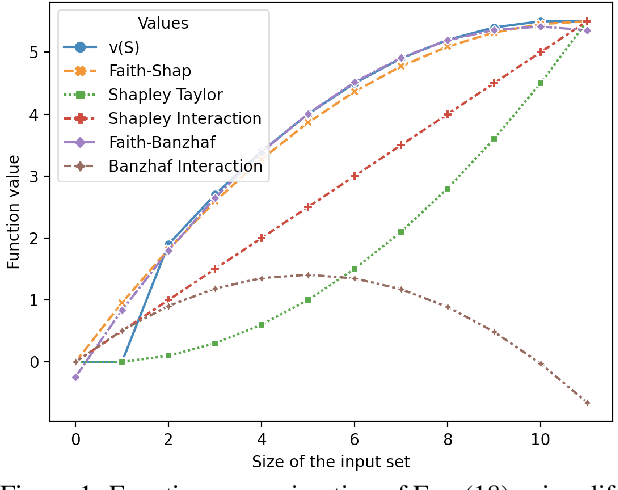

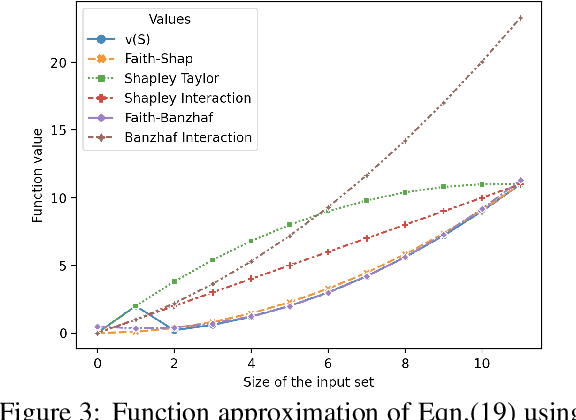
Shapley values, which were originally designed to assign attributions to individual players in coalition games, have become a commonly used approach in explainable machine learning to provide attributions to input features for black-box machine learning models. A key attraction of Shapley values is that they uniquely satisfy a very natural set of axiomatic properties. However, extending the Shapley value to assigning attributions to interactions rather than individual players, an interaction index, is non-trivial: as the natural set of axioms for the original Shapley values, extended to the context of interactions, no longer specify a unique interaction index. Many proposals thus introduce additional less "natural" axioms, while sacrificing the key axiom of efficiency, in order to obtain unique interaction indices. In this work, rather than introduce additional conflicting axioms, we adopt the viewpoint of Shapley values as coefficients of the most faithful linear approximation to the pseudo-Boolean coalition game value function. By extending linear to $\ell$-order polynomial approximations, we can then define the general family of faithful interaction indices}. We show that by additionally requiring the faithful interaction indices to satisfy interaction-extensions of the standard individual Shapley axioms (dummy, symmetry, linearity, and efficiency), we obtain a unique FaithfulShapley Interaction index, which we denote Faith-Shap, as a natural generalization of the Shapley value to interactions. We then provide some illustrative contrasts of Faith-Shap with previously proposed interaction indices, and further investigate some of its interesting algebraic properties. We further show the computational efficiency of computing Faith-Shap, together with some additional qualitative insights, via some illustrative experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge