Fair clustering via equitable group representations
Paper and Code
Jun 19, 2020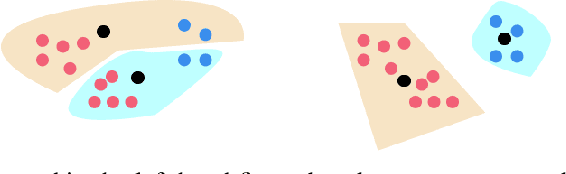

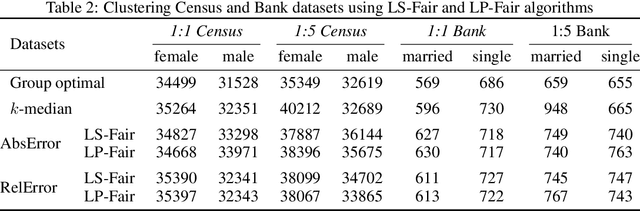
What does it mean for a clustering to be fair? One popular approach seeks to ensure that each cluster contains groups in (roughly) the same proportion in which they exist in the population. The normative principle at play is balance: any cluster might act as a representative of the data, and thus should reflect its diversity. But clustering also captures a different form of representativeness. A core principle in most clustering problems is that a cluster center should be representative of the cluster it represents, by being "close" to the points associated with it. This is so that we can effectively replace the points by their cluster centers without significant loss in fidelity, and indeed is a common "use case" for clustering. For such a clustering to be fair, the centers should "represent" different groups equally well. We call such a clustering a group-representative clustering. In this paper, we study the structure and computation of group-representative clusterings. We show that this notion naturally parallels the development of fairness notions in classification, with direct analogs of ideas like demographic parity and equal opportunity. We demonstrate how these notions are distinct from and cannot be captured by balance-based notions of fairness. We present approximation algorithms for group representative $k$-median clustering and couple this with an empirical evaluation on various real-world data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge