Extendable and invertible manifold learning with geometry regularized autoencoders

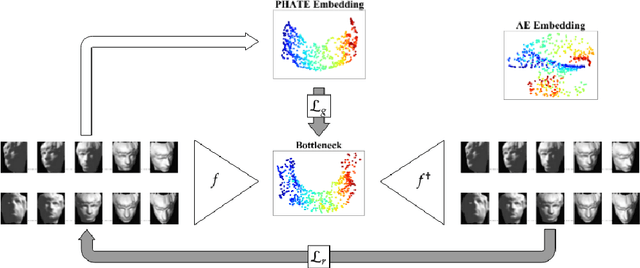
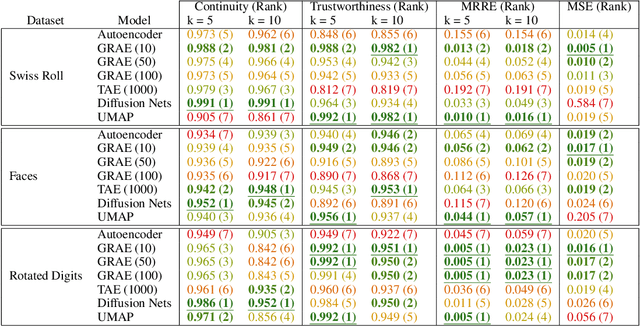
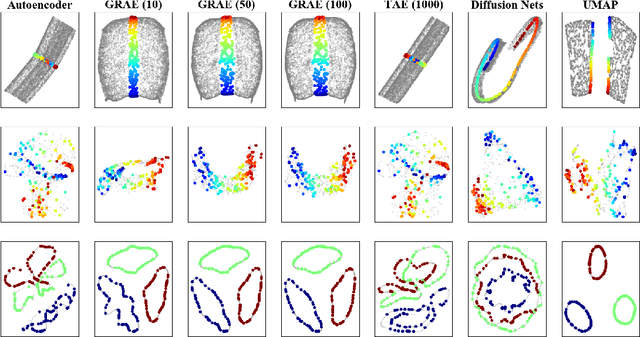
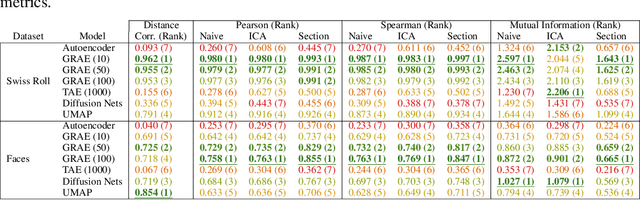
A fundamental task in data exploration is to extract simplified low dimensional representations that capture intrinsic geometry in data, especially for the purpose of faithfully visualizing data in two or three dimensions. Common approaches to this task use kernel methods for manifold learning. However, these methods typically only provide an embedding of fixed input data and cannot extend to new data points. On the other hand, autoencoders have recently become widely popular for representation learning, but while they naturally compute feature extractors that are both extendable to new data and invertible (i.e., reconstructing original features from latent representation), they provide limited capabilities to follow global intrinsic geometry compared to kernel-based manifold learning. Here, we present a new method for integrating both approaches by incorporating a geometric regularization term in the bottleneck of the autoencoder. Our regularization, based on the diffusion potential distances from the recently-proposed PHATE visualization method, encourages the learned latent representation to follow intrinsic data geometry, similar to manifold learning algorithms, while still enabling faithful extension to new data and reconstruction of data in the original feature space from latent coordinates. We compare our approach with leading kernel methods and autoencoder models for manifold learning to provide qualitative and quantitative evidence of our advantages in preserving intrinsic structure, out of sample extension, and reconstruction.