Exploring Unified Perspective For Fast Shapley Value Estimation
Paper and Code
Nov 02, 2023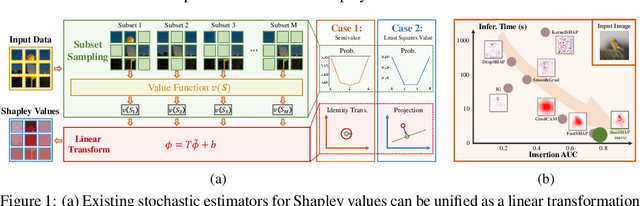


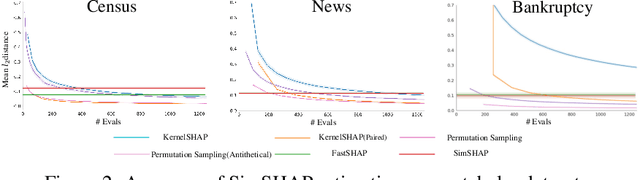
Shapley values have emerged as a widely accepted and trustworthy tool, grounded in theoretical axioms, for addressing challenges posed by black-box models like deep neural networks. However, computing Shapley values encounters exponential complexity in the number of features. Various approaches, including ApproSemivalue, KernelSHAP, and FastSHAP, have been explored to expedite the computation. We analyze the consistency of existing works and conclude that stochastic estimators can be unified as the linear transformation of importance sampling of feature subsets. Based on this, we investigate the possibility of designing simple amortized estimators and propose a straightforward and efficient one, SimSHAP, by eliminating redundant techniques. Extensive experiments conducted on tabular and image datasets validate the effectiveness of our SimSHAP, which significantly accelerates the computation of accurate Shapley values.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge