Exploration by Maximizing Rényi Entropy for Zero-Shot Meta RL

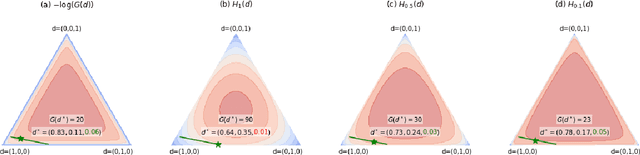
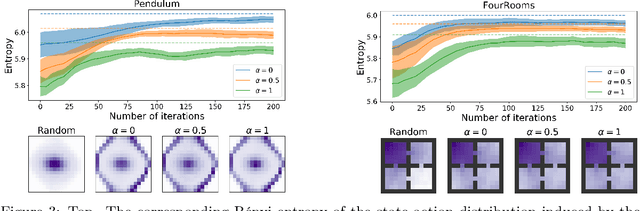
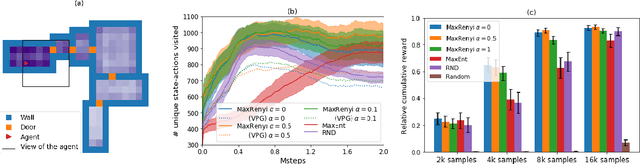
Exploring the transition dynamics is essential to the success of reinforcement learning (RL) algorithms. To face the challenges of exploration, we consider a zero-shot meta RL framework that completely separates exploration from exploitation and is suitable for the meta RL setting where there are many reward functions of interest. In the exploration phase, the agent learns an exploratory policy by interacting with a reward-free environment and collects a dataset of transitions by executing the policy. In the planning phase, the agent computes a good policy for any reward function based on the dataset without further interacting with the environment. This framework brings new challenges for exploration algorithms. In the exploration phase, we propose to maximize the R\'enyi entropy over the state-action space and justify this objective theoretically. We further deduce a policy gradient formulation for this objective and design a practical exploration algorithm that can deal with complex environments based on PPO. In the planning phase, we use a batch RL algorithm, batch constrained deep Q-learning (BCQ), to solve for good policies given arbitrary reward functions. Empirically, we show that our exploration algorithm is effective and sample efficient, and results in superior policies for arbitrary reward functions in the planning phase.