Exploiting the Natural Dynamics of Series Elastic Robots by Actuator-Centered Sequential Linear Programming
Paper and Code
Jul 17, 2018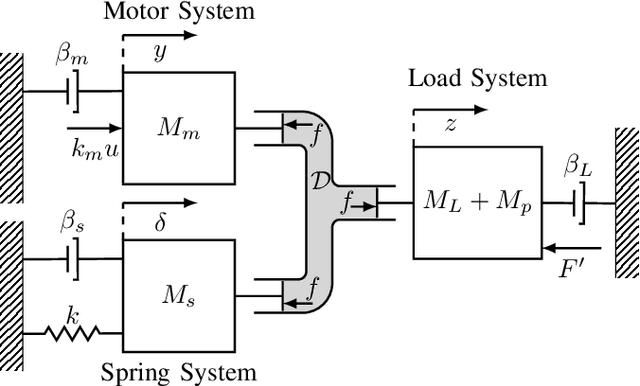
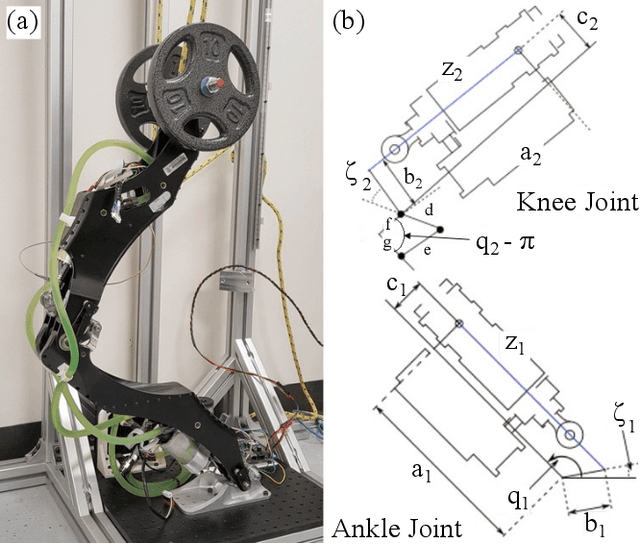
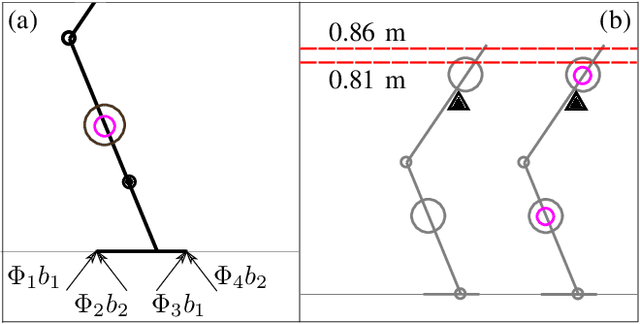
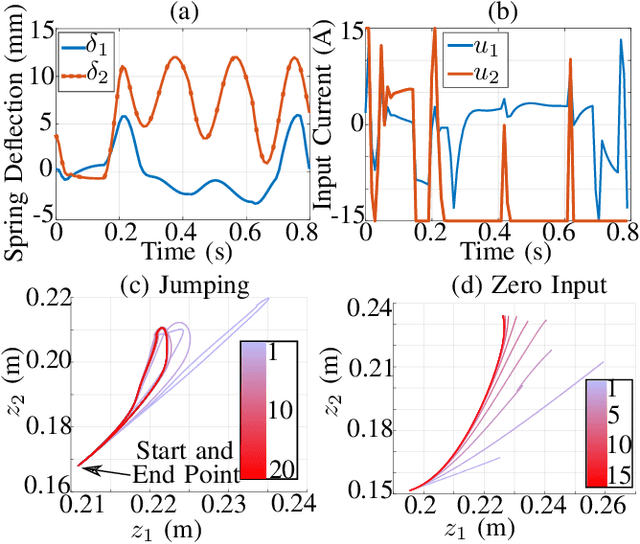
Series elastic robots are best able to follow trajectories which obey the limitations of their actuators, since they cannot instantly change their joint forces. In fact, the performance of series elastic actuators can surpass that of ideal force source actuators by storing and releasing energy. In this paper, we formulate the trajectory optimization problem for series elastic robots in a novel way based on sequential linear programming. Our framework is unique in the separation of the actuator dynamics from the rest of the dynamics, and in the use of a tunable pseudo-mass parameter that improves the discretization accuracy of our approach. The actuator dynamics are truly linear, which allows them to be excluded from trust-region mechanics. This causes our algorithm to have similar run times with and without the actuator dynamics. We demonstrate our optimization algorithm by tuning high performance behaviors for a single-leg robot in simulation and on hardware for a single degree-of-freedom actuator testbed. The results show that compliance allows for faster motions and takes a similar amount of computation time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge