Exploiting skeletal structure in computer vision annotation with Benders decomposition
Paper and Code
Sep 13, 2017
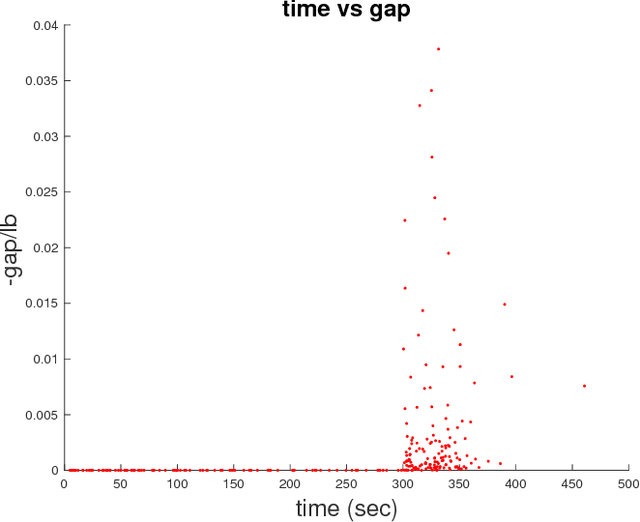
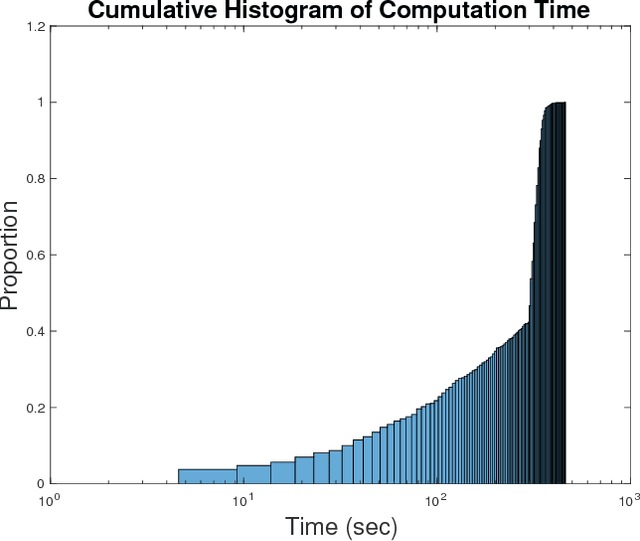

Many annotation problems in computer vision can be phrased as integer linear programs (ILPs). The use of standard industrial solvers does not to exploit the underlying structure of such problems eg, the skeleton in pose estimation. The leveraging of the underlying structure in conjunction with industrial solvers promises increases in both speed and accuracy. Such structure can be exploited using Bender's decomposition, a technique from operations research, that solves complex ILPs or mixed integer linear programs by decomposing them into sub-problems that communicate via a master problem. The intuition is that conditioned on a small subset of the variables the solution to the remaining variables can be computed easily by taking advantage of properties of the ILP constraint matrix such as block structure. In this paper we apply Benders decomposition to a typical problem in computer vision where we have many sub-ILPs (eg, partitioning of detections, body-parts) coupled to a master ILP (eg, constructing skeletons). Dividing inference problems into a master problem and sub-problems motivates the development of a plethora of novel models, and inference approaches for the field of computer vision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge