Exploiting Problem Structure in Deep Declarative Networks: Two Case Studies
Paper and Code
Feb 24, 2022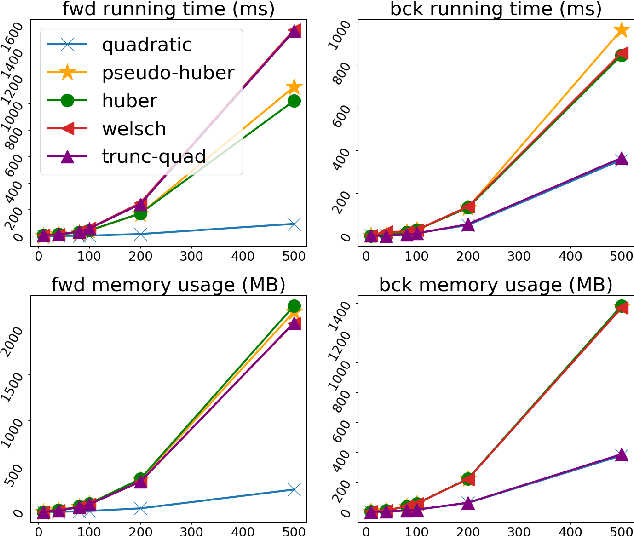
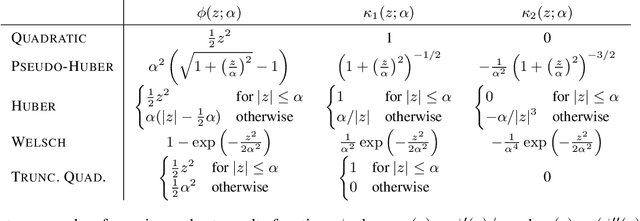

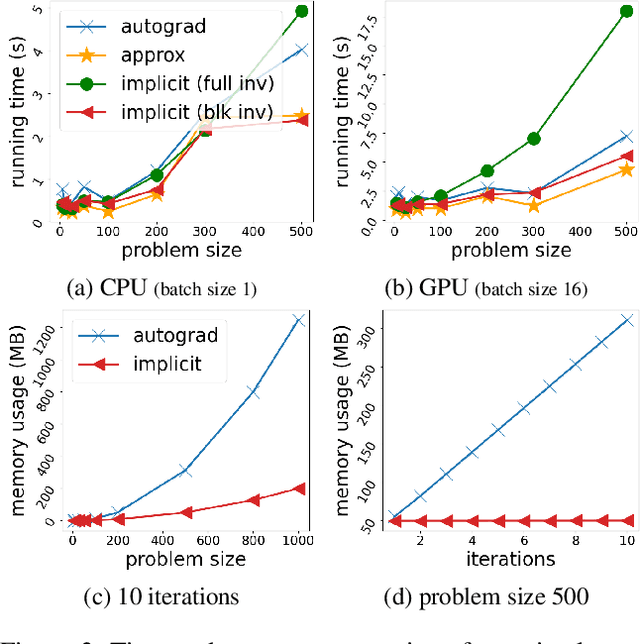
Deep declarative networks and other recent related works have shown how to differentiate the solution map of a (continuous) parametrized optimization problem, opening up the possibility of embedding mathematical optimization problems into end-to-end learnable models. These differentiability results can lead to significant memory savings by providing an expression for computing the derivative without needing to unroll the steps of the forward-pass optimization procedure during the backward pass. However, the results typically require inverting a large Hessian matrix, which is computationally expensive when implemented naively. In this work we study two applications of deep declarative networks -- robust vector pooling and optimal transport -- and show how problem structure can be exploited to obtain very efficient backward pass computations in terms of both time and memory. Our ideas can be used as a guide for improving the computational performance of other novel deep declarative nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge