Evolution of Novel Activation Functions in Neural Network Training with Applications to Classification of Exoplanets
Paper and Code
Jun 01, 2019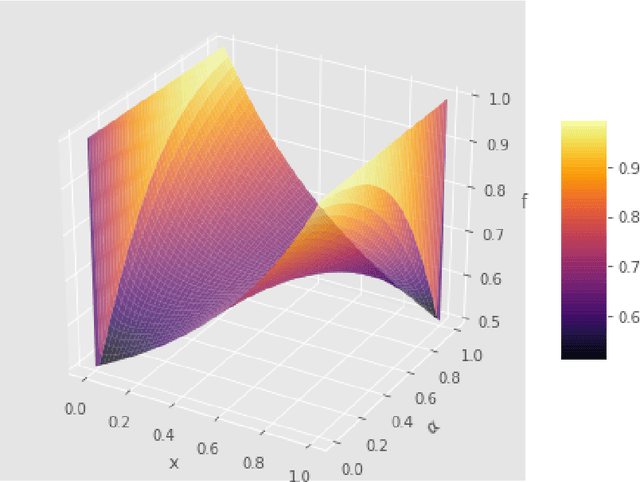
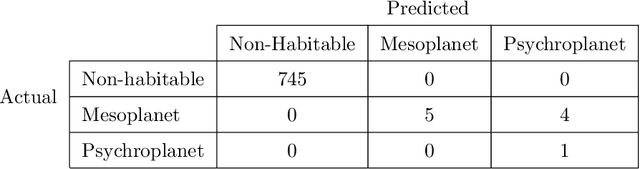
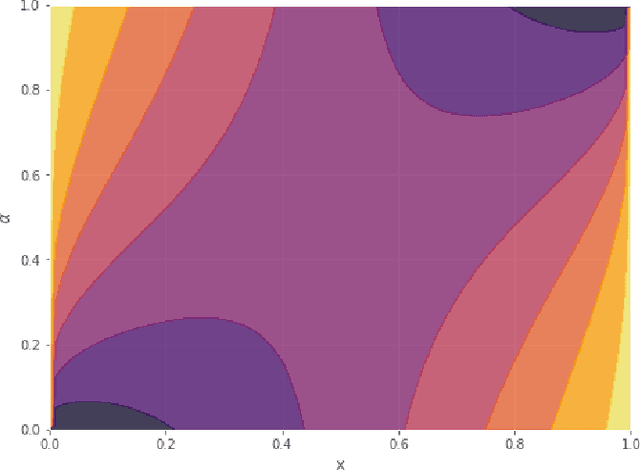
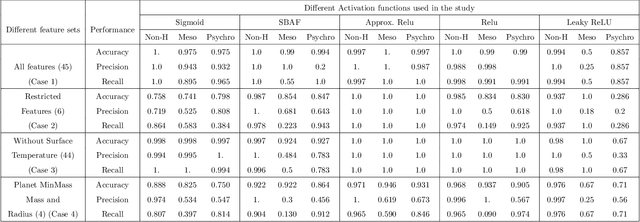
We present analytical exploration of novel activation functions as consequence of integration of several ideas leading to implementation and subsequent use in habitability classification of exoplanets. Neural networks, although a powerful engine in supervised methods, often require expensive tuning efforts for optimized performance. Habitability classes are hard to discriminate, especially when attributes used as hard markers of separation are removed from the data set. The solution is approached from the point of investigating analytical properties of the proposed activation functions. The theory of ordinary differential equations and fixed point are exploited to justify the "lack of tuning efforts" to achieve optimal performance compared to traditional activation functions. Additionally, the relationship between the proposed activation functions and the more popular ones is established through extensive analytical and empirical evidence. Finally, the activation functions have been implemented in plain vanilla feed-forward neural network to classify exoplanets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge