Evidential Softmax for Sparse Multimodal Distributions in Deep Generative Models
Paper and Code
Oct 27, 2021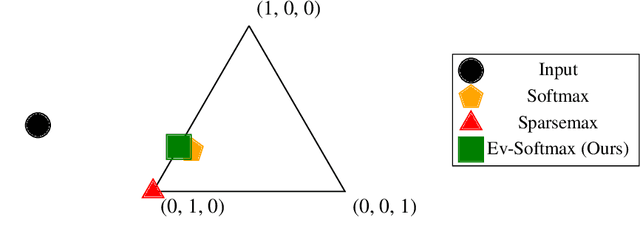

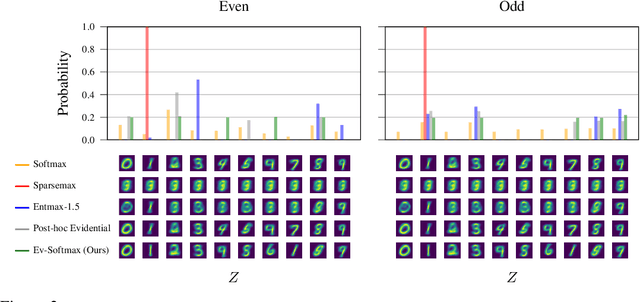
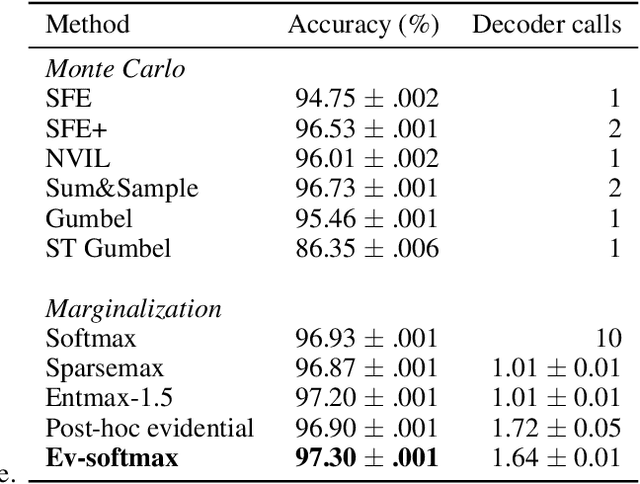
Many applications of generative models rely on the marginalization of their high-dimensional output probability distributions. Normalization functions that yield sparse probability distributions can make exact marginalization more computationally tractable. However, sparse normalization functions usually require alternative loss functions for training since the log-likelihood is undefined for sparse probability distributions. Furthermore, many sparse normalization functions often collapse the multimodality of distributions. In this work, we present $\textit{ev-softmax}$, a sparse normalization function that preserves the multimodality of probability distributions. We derive its properties, including its gradient in closed-form, and introduce a continuous family of approximations to $\textit{ev-softmax}$ that have full support and can be trained with probabilistic loss functions such as negative log-likelihood and Kullback-Leibler divergence. We evaluate our method on a variety of generative models, including variational autoencoders and auto-regressive architectures. Our method outperforms existing dense and sparse normalization techniques in distributional accuracy. We demonstrate that $\textit{ev-softmax}$ successfully reduces the dimensionality of probability distributions while maintaining multimodality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge