Evaluating time series forecasting models: An empirical study on performance estimation methods
Paper and Code
May 28, 2019

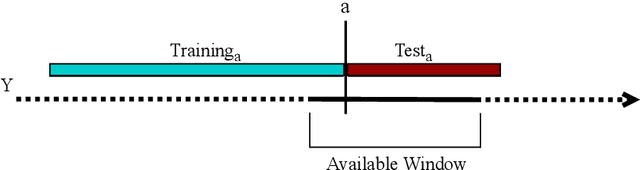
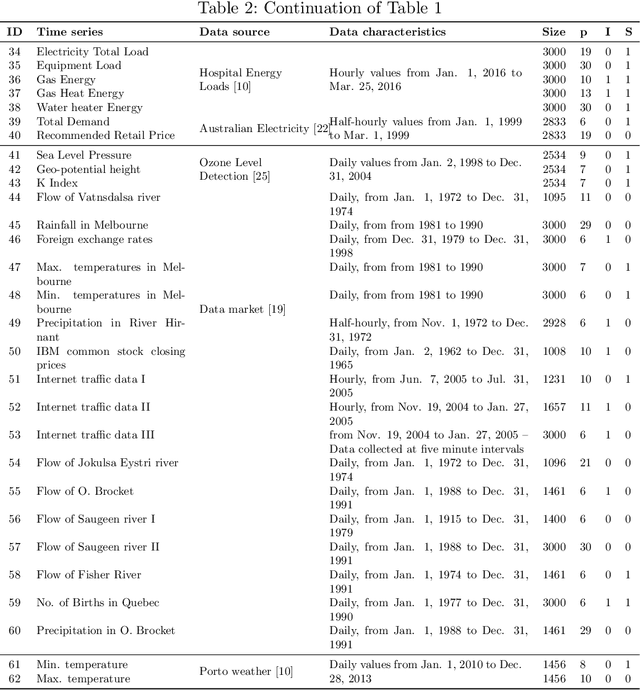
Performance estimation aims at estimating the loss that a predictive model will incur on unseen data. These procedures are part of the pipeline in every machine learning project and are used for assessing the overall generalisation ability of predictive models. In this paper we address the application of these methods to time series forecasting tasks. For independent and identically distributed data the most common approach is cross-validation. However, the dependency among observations in time series raises some caveats about the most appropriate way to estimate performance in this type of data and currently there is no settled way to do so. We compare different variants of cross-validation and of out-of-sample approaches using two case studies: One with 62 real-world time series and another with three synthetic time series. Results show noticeable differences in the performance estimation methods in the two scenarios. In particular, empirical experiments suggest that cross-validation approaches can be applied to stationary time series. However, in real-world scenarios, when different sources of non-stationary variation are at play, the most accurate estimates are produced by out-of-sample methods that preserve the temporal order of observations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge