Evaluating State-of-the-Art Classification Models Against Bayes Optimality
Paper and Code
Jun 07, 2021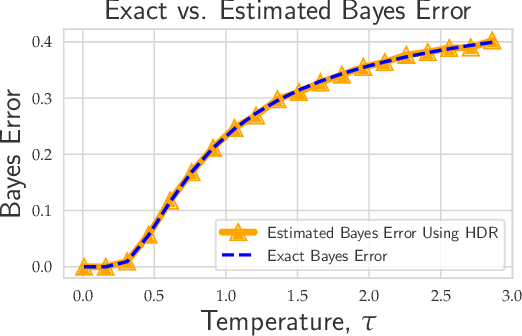
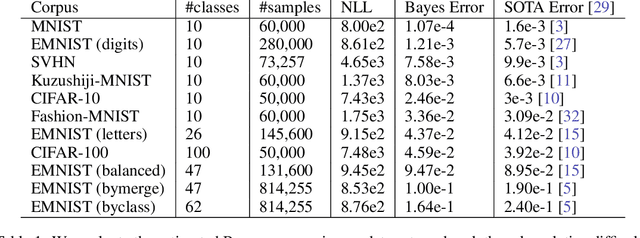

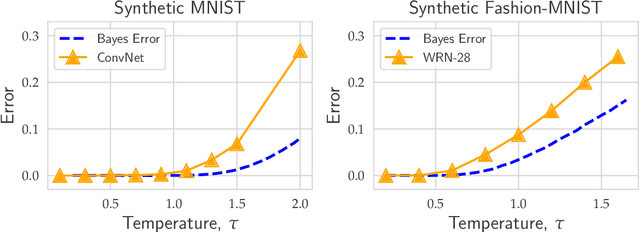
Evaluating the inherent difficulty of a given data-driven classification problem is important for establishing absolute benchmarks and evaluating progress in the field. To this end, a natural quantity to consider is the \emph{Bayes error}, which measures the optimal classification error theoretically achievable for a given data distribution. While generally an intractable quantity, we show that we can compute the exact Bayes error of generative models learned using normalizing flows. Our technique relies on a fundamental result, which states that the Bayes error is invariant under invertible transformation. Therefore, we can compute the exact Bayes error of the learned flow models by computing it for Gaussian base distributions, which can be done efficiently using Holmes-Diaconis-Ross integration. Moreover, we show that by varying the temperature of the learned flow models, we can generate synthetic datasets that closely resemble standard benchmark datasets, but with almost any desired Bayes error. We use our approach to conduct a thorough investigation of state-of-the-art classification models, and find that in some -- but not all -- cases, these models are capable of obtaining accuracy very near optimal. Finally, we use our method to evaluate the intrinsic "hardness" of standard benchmark datasets, and classes within those datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge