Estimation of embedding vectors in high dimensions
Paper and Code
Dec 12, 2023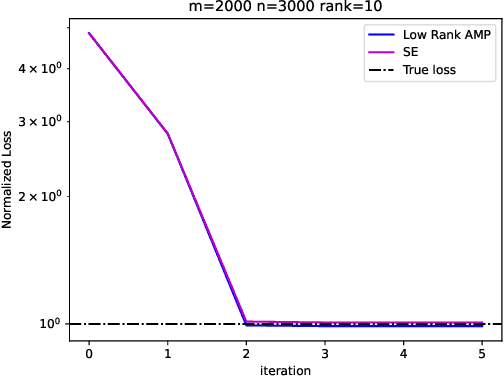
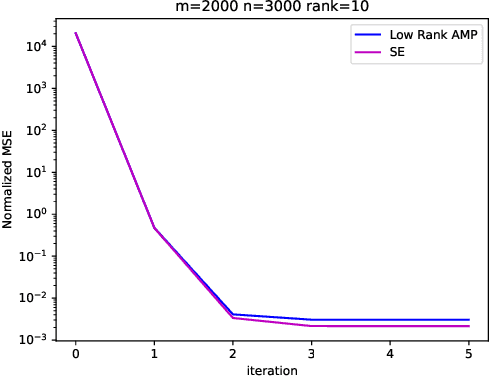
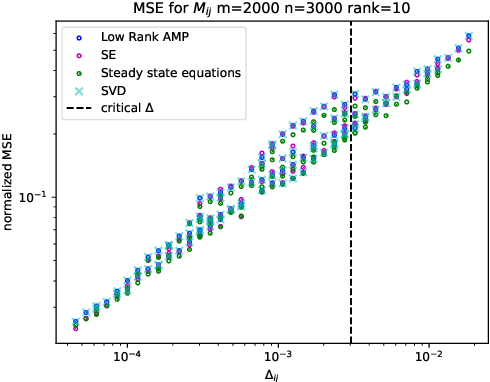
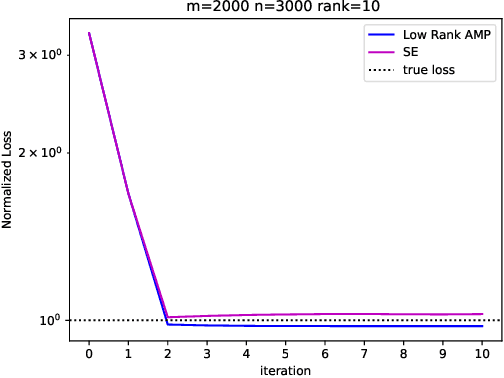
Embeddings are a basic initial feature extraction step in many machine learning models, particularly in natural language processing. An embedding attempts to map data tokens to a low-dimensional space where similar tokens are mapped to vectors that are close to one another by some metric in the embedding space. A basic question is how well can such embedding be learned? To study this problem, we consider a simple probability model for discrete data where there is some "true" but unknown embedding where the correlation of random variables is related to the similarity of the embeddings. Under this model, it is shown that the embeddings can be learned by a variant of low-rank approximate message passing (AMP) method. The AMP approach enables precise predictions of the accuracy of the estimation in certain high-dimensional limits. In particular, the methodology provides insight on the relations of key parameters such as the number of samples per value, the frequency of the terms, and the strength of the embedding correlation on the probability distribution. Our theoretical findings are validated by simulations on both synthetic data and real text data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge