Estimation, Confidence Intervals, and Large-Scale Hypotheses Testing for High-Dimensional Mixed Linear Regression

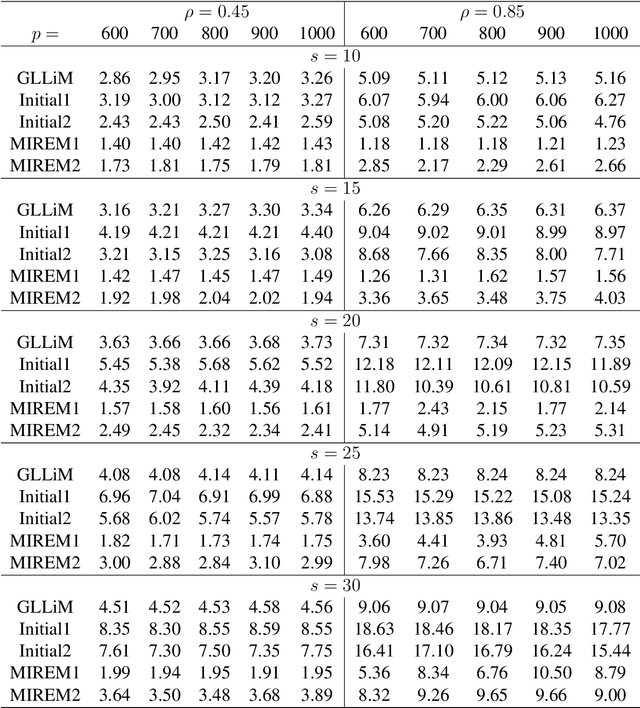
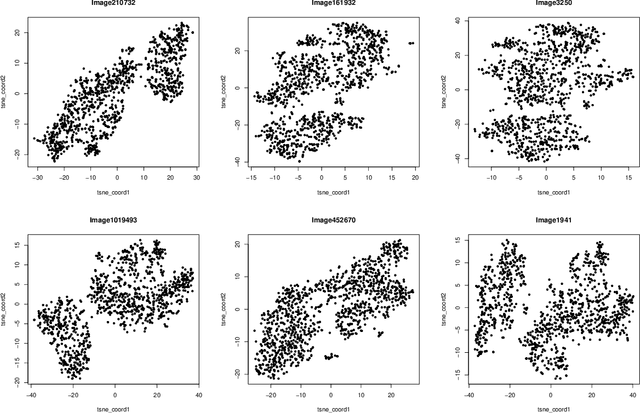
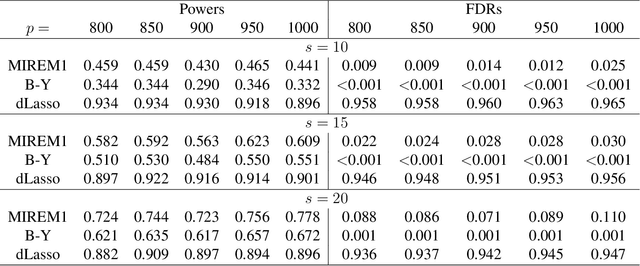
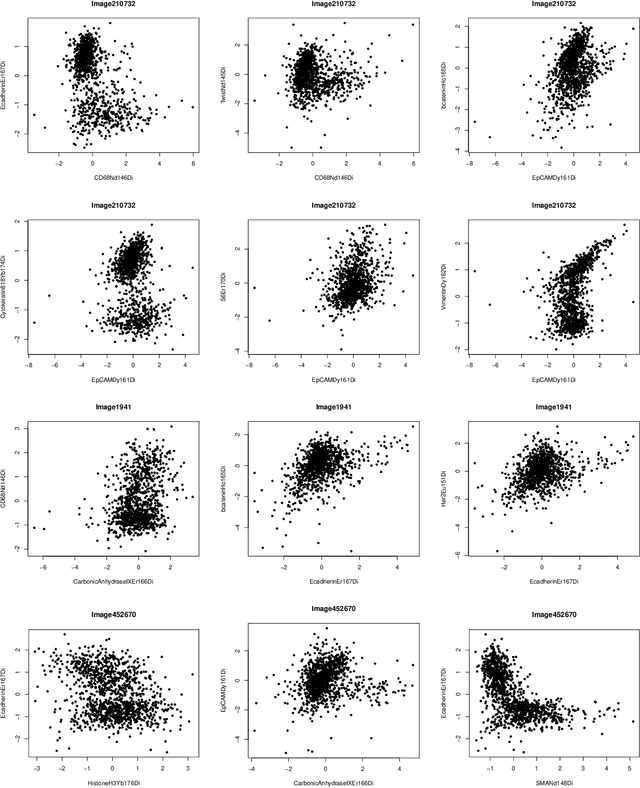
This paper studies the high-dimensional mixed linear regression (MLR) where the output variable comes from one of the two linear regression models with an unknown mixing proportion and an unknown covariance structure of the random covariates. Building upon a high-dimensional EM algorithm, we propose an iterative procedure for estimating the two regression vectors and establish their rates of convergence. Based on the iterative estimators, we further construct debiased estimators and establish their asymptotic normality. For individual coordinates, confidence intervals centered at the debiased estimators are constructed. Furthermore, a large-scale multiple testing procedure is proposed for testing the regression coefficients and is shown to control the false discovery rate (FDR) asymptotically. Simulation studies are carried out to examine the numerical performance of the proposed methods and their superiority over existing methods. The proposed methods are further illustrated through an analysis of a dataset of multiplex image cytometry, which investigates the interaction networks among the cellular phenotypes that include the expression levels of 20 epitopes or combinations of markers.