Equilibrated Recurrent Neural Network: Neuronal Time-Delayed Self-Feedback Improves Accuracy and Stability

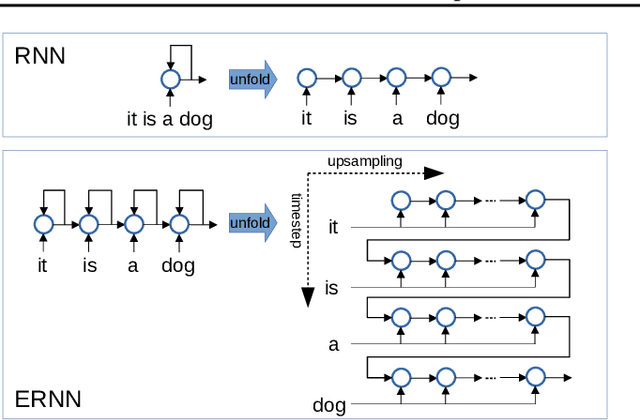
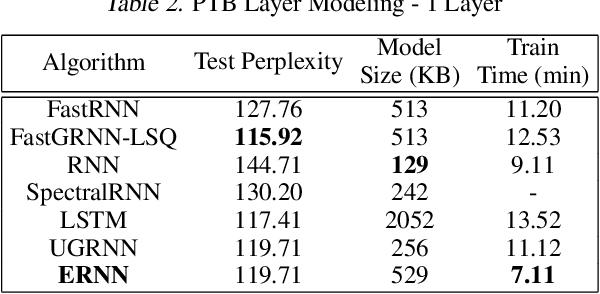
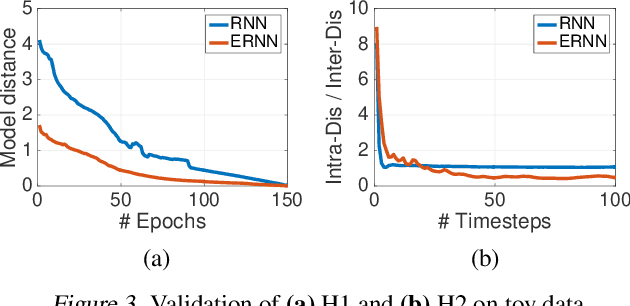
We propose a novel {\it Equilibrated Recurrent Neural Network} (ERNN) to combat the issues of inaccuracy and instability in conventional RNNs. Drawing upon the concept of autapse in neuroscience, we propose augmenting an RNN with a time-delayed self-feedback loop. Our sole purpose is to modify the dynamics of each internal RNN state and, at any time, enforce it to evolve close to the equilibrium point associated with the input signal at that time. We show that such self-feedback helps stabilize the hidden state transitions leading to fast convergence during training while efficiently learning discriminative latent features that result in state-of-the-art results on several benchmark datasets at test-time. We propose a novel inexact Newton method to solve fixed-point conditions given model parameters for generating the latent features at each hidden state. We prove that our inexact Newton method converges locally with linear rate (under mild conditions). We leverage this result for efficient training of ERNNs based on backpropagation.