Epistemic Exploration for Generalizable Planning and Learning in Non-Stationary Settings

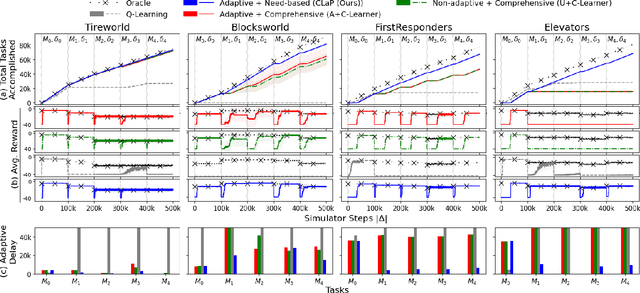
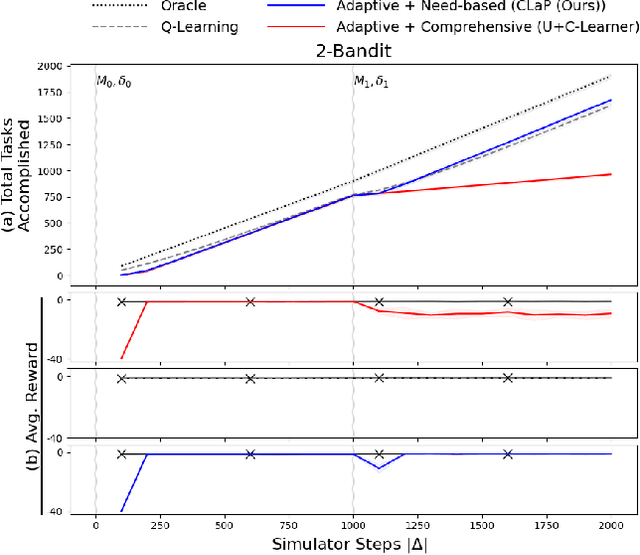
This paper introduces a new approach for continual planning and model learning in non-stationary stochastic environments expressed using relational representations. Such capabilities are essential for the deployment of sequential decision-making systems in the uncertain, constantly evolving real world. Working in such practical settings with unknown (and non-stationary) transition systems and changing tasks, the proposed framework models gaps in the agent's current state of knowledge and uses them to conduct focused, investigative explorations. Data collected using these explorations is used for learning generalizable probabilistic models for solving the current task despite continual changes in the environment dynamics. Empirical evaluations on several benchmark domains show that this approach significantly outperforms planning and RL baselines in terms of sample complexity in non-stationary settings. Theoretical results show that the system reverts to exhibit desirable convergence properties when stationarity holds.