Enhanced Robot Motion Block of A-star Algorithm for Robotic Path Planning
Paper and Code
Dec 25, 2023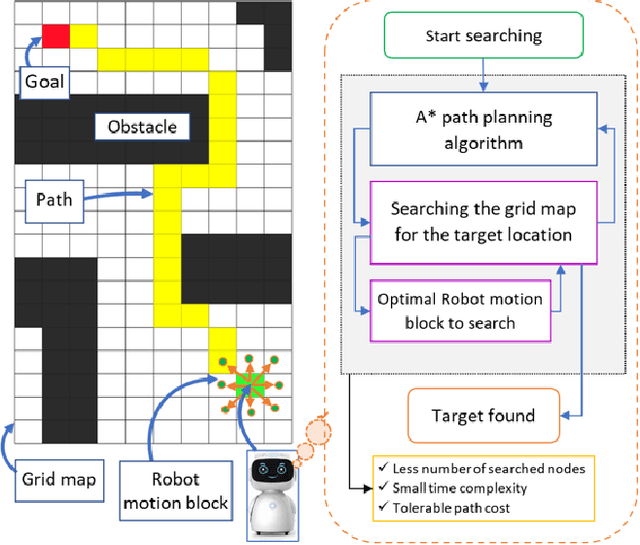
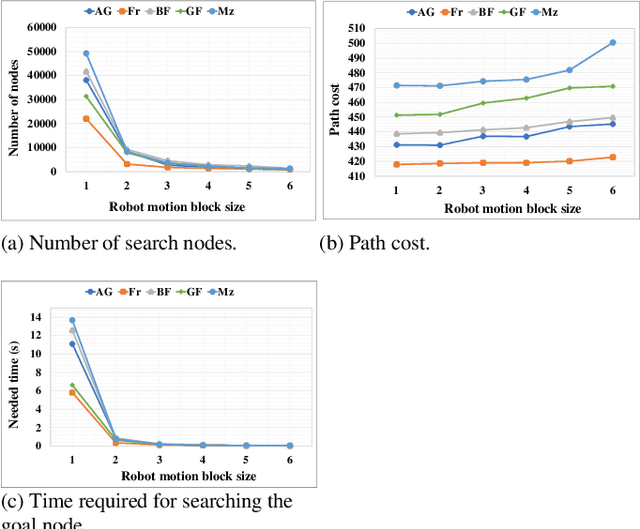

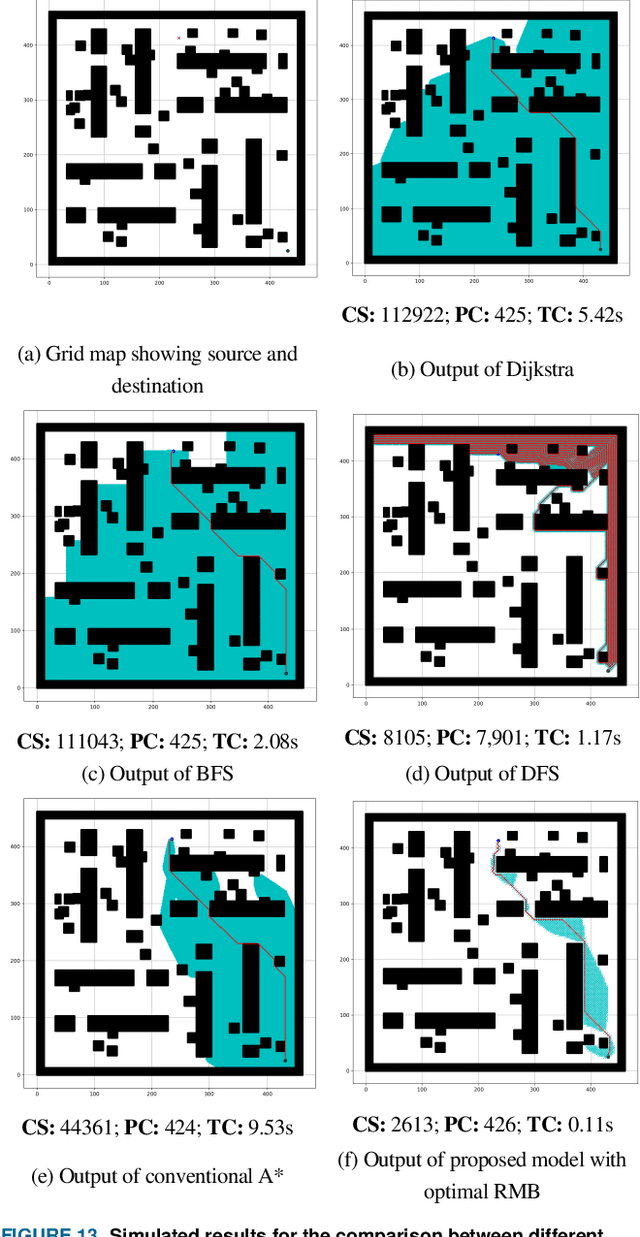
An efficient robot path-planning model is vulnerable to the number of search nodes, path cost, and time complexity. The conventional A-star (A*) algorithm outperforms other grid-based algorithms for its heuristic search. However it shows suboptimal performance for the time, space, and number of search nodes, depending on the robot motion block (RMB). To address this challenge, this study proposes an optimal RMB for the A* path-planning algorithm to enhance the performance, where the robot movement costs are calculated by the proposed adaptive cost function. Also, a selection process is proposed to select the optimal RMB size. In this proposed model, grid-based maps are used, where the robot's next move is determined based on the adaptive cost function by searching among surrounding octet neighborhood grid cells. The cumulative value from the output data arrays is used to determine the optimal motion block size, which is formulated based on parameters. The proposed RMB significantly affects the searching time complexity and number of search nodes of the A* algorithm while maintaining almost the same path cost to find the goal position by avoiding obstacles. For the experiment, a benchmarked online dataset is used and prepared three different dimensional maps. The proposed approach is validated using approximately 7000 different grid maps with various dimensions and obstacle environments. The proposed model with an optimal RMB demonstrated a remarkable improvement of 93.98% in the number of search cells and 98.94% in time complexity compared to the conventional A* algorithm. Path cost for the proposed model remained largely comparable to other state-of-the-art algorithms. Also, the proposed model outperforms other state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge