Enabling arbitrary translation objectives with Adaptive Tree Search
Paper and Code
Feb 23, 2022
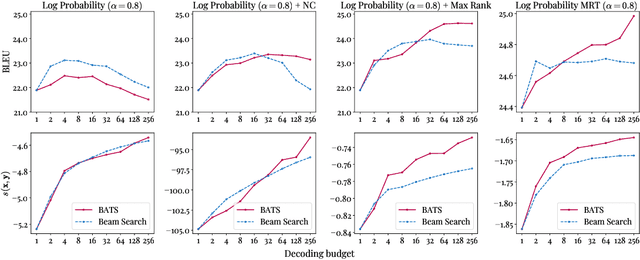
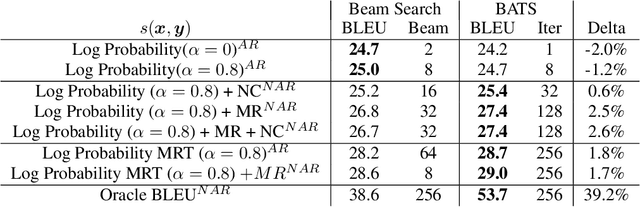
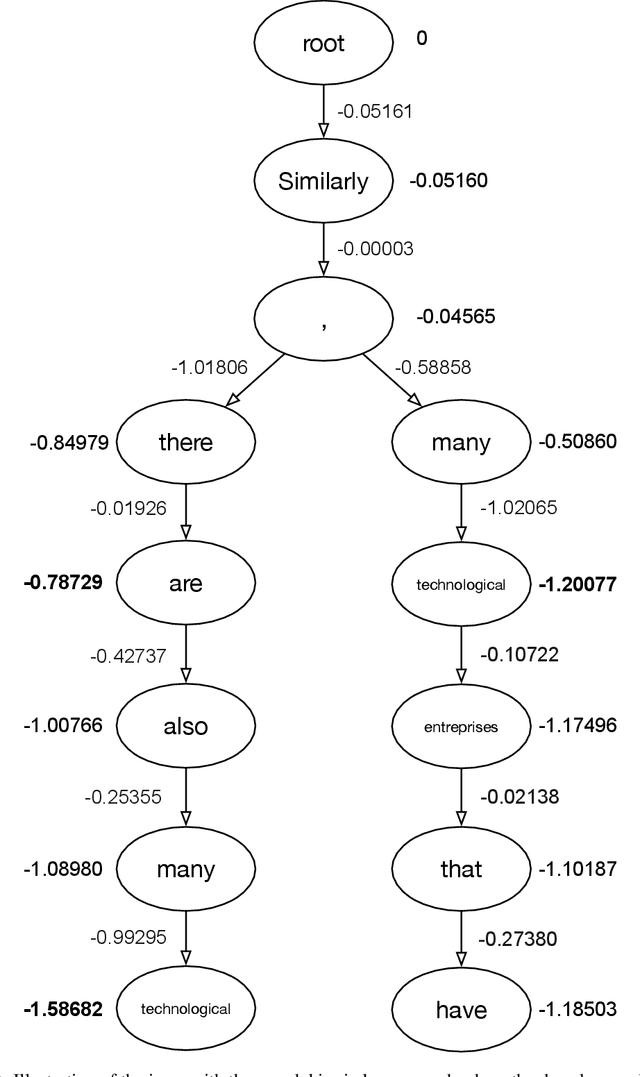
We introduce an adaptive tree search algorithm, that can find high-scoring outputs under translation models that make no assumptions about the form or structure of the search objective. This algorithm -- a deterministic variant of Monte Carlo tree search -- enables the exploration of new kinds of models that are unencumbered by constraints imposed to make decoding tractable, such as autoregressivity or conditional independence assumptions. When applied to autoregressive models, our algorithm has different biases than beam search has, which enables a new analysis of the role of decoding bias in autoregressive models. Empirically, we show that our adaptive tree search algorithm finds outputs with substantially better model scores compared to beam search in autoregressive models, and compared to reranking techniques in models whose scores do not decompose additively with respect to the words in the output. We also characterise the correlation of several translation model objectives with respect to BLEU. We find that while some standard models are poorly calibrated and benefit from the beam search bias, other often more robust models (autoregressive models tuned to maximize expected automatic metric scores, the noisy channel model and a newly proposed objective) benefit from increasing amounts of search using our proposed decoder, whereas the beam search bias limits the improvements obtained from such objectives. Thus, we argue that as models improve, the improvements may be masked by over-reliance on beam search or reranking based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge