Ellipsoidal Trust Region Methods and the Marginal Value of Hessian Information for Neural Network Training
Paper and Code
May 22, 2019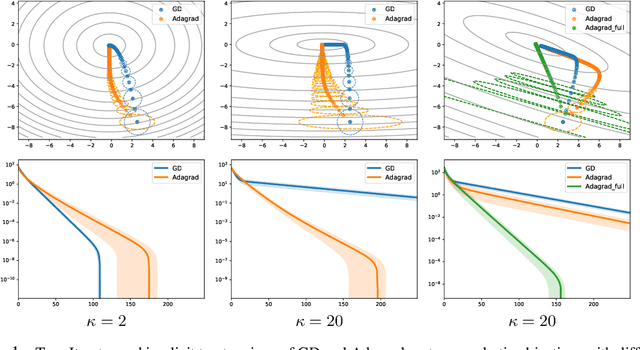

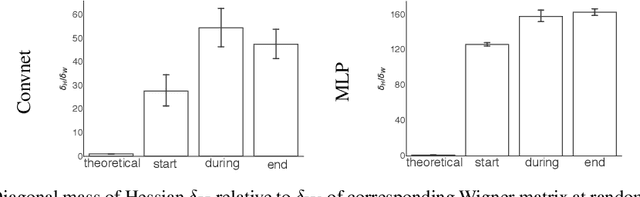
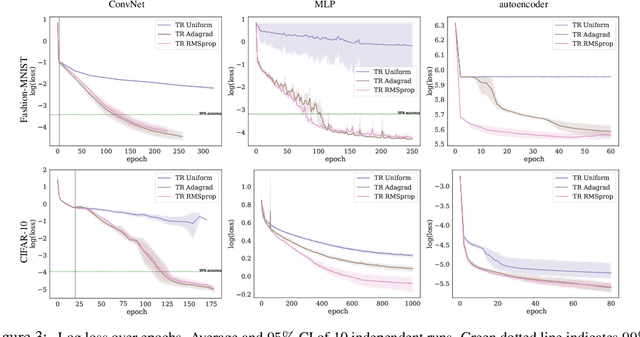
We investigate the use of ellipsoidal trust region constraints for second-order optimization of neural networks. This approach can be seen as a higher-order counterpart of adaptive gradient methods, which we here show to be interpretable as first-order trust region methods with ellipsoidal constraints. In particular, we show that the preconditioning matrix used in RMSProp and Adam satisfies the necessary conditions for convergence of (first- and) second-order trust region methods and report that this ellipsoidal constraint constantly outperforms its spherical counterpart in practice. We furthermore set out to clarify the long-standing question of the potential superiority of Newton methods in deep learning. In this regard, we run extensive benchmarks across different datasets and architectures to find that comparable performance to gradient descent algorithms can be achieved but using Hessian information does not give rise to better limit points and comes at the cost of increased hyperparameter tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge