EIS -- a family of activation functions combining Exponential, ISRU, and Softplus

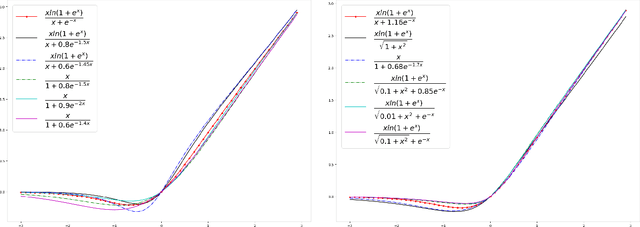
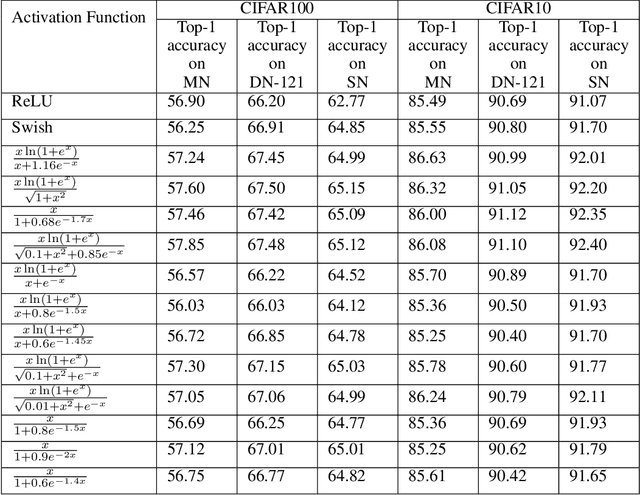
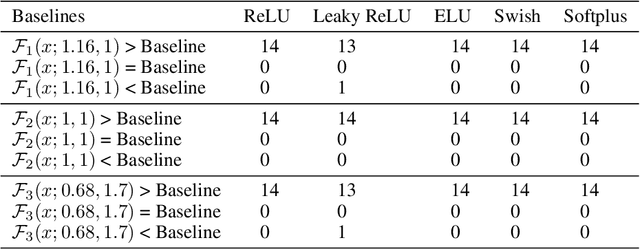
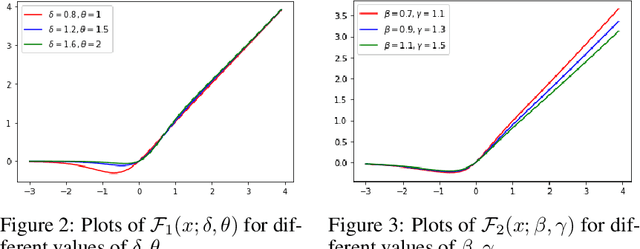
Activation functions play a pivotal role in the function learning using neural networks. The non-linearity in the learned function is achieved by repeated use of the activation function. Over the years, numerous activation functions have been proposed to improve accuracy in several tasks. Basic functions like ReLU, Sigmoid, Tanh, or Softplus have been favorite among the deep learning community because of their simplicity. In recent years, several novel activation functions arising from these basic functions have been proposed, which have improved accuracy in some challenging datasets. We propose a five hyper-parameters family of activation functions, namely EIS, defined as, \[ \frac{x(\ln(1+e^x))^\alpha}{\sqrt{\beta+\gamma x^2}+\delta e^{-\theta x}}. \] We show examples of activation functions from the EIS family which outperform widely used activation functions on some well known datasets and models. For example, $\frac{x\ln(1+e^x)}{x+1.16e^{-x}}$ beats ReLU by 0.89\% in DenseNet-169, 0.24\% in Inception V3 in CIFAR100 dataset while 1.13\% in Inception V3, 0.13\% in DenseNet-169, 0.94\% in SimpleNet model in CIFAR10 dataset. Also, $\frac{x\ln(1+e^x)}{\sqrt{1+x^2}}$ beats ReLU by 1.68\% in DenseNet-169, 0.30\% in Inception V3 in CIFAR100 dataset while 1.0\% in Inception V3, 0.15\% in DenseNet-169, 1.13\% in SimpleNet model in CIFAR10 dataset.