Effort Allocation for Deadline-Aware Task and Motion Planning: A Metareasoning Approach
Paper and Code
Oct 08, 2024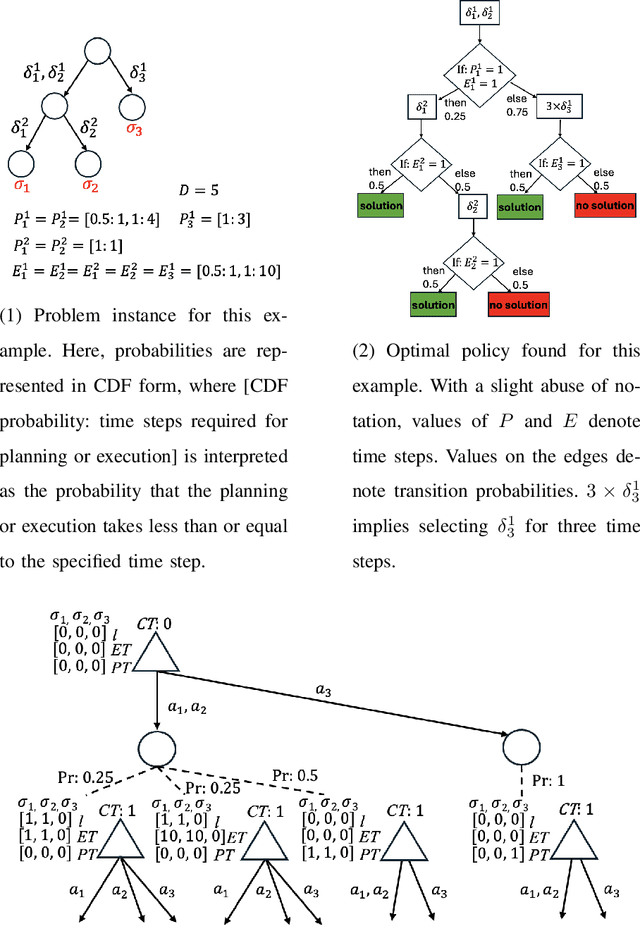


In robot planning, tasks can often be achieved through multiple options, each consisting of several actions. This work specifically addresses deadline constraints in task and motion planning, aiming to find a plan that can be executed within the deadline despite uncertain planning and execution times. We propose an effort allocation problem, formulated as a Markov decision process (MDP), to find such a plan by leveraging metareasoning perspectives to allocate computational resources among the given options. We formally prove the NP-hardness of the problem by reducing it from the knapsack problem. Both a model-based approach, where transition models are learned from past experience, and a model-free approach, which overcomes the unavailability of prior data acquisition through reinforcement learning, are explored. For the model-based approach, we investigate Monte Carlo tree search (MCTS) to approximately solve the proposed MDP and further design heuristic schemes to tackle NP-hardness, leading to the approximate yet efficient algorithm called DP_Rerun. In experiments, DP_Rerun demonstrates promising performance comparable to MCTS while requiring negligible computation time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge