Efficient Privacy-Preserving Nonconvex Optimization

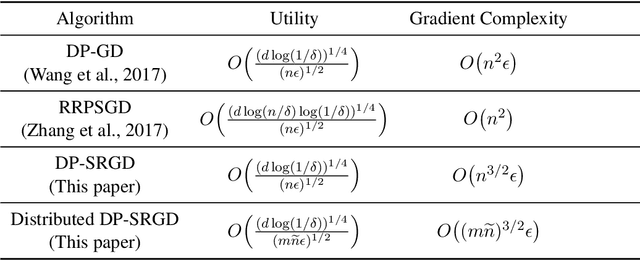
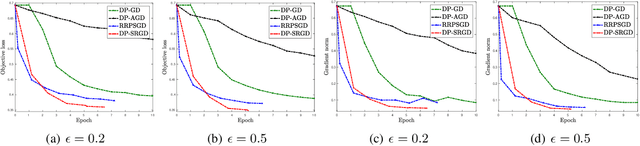
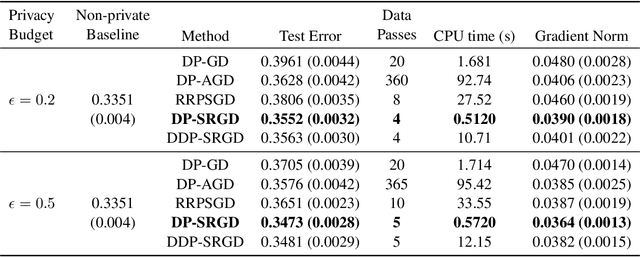
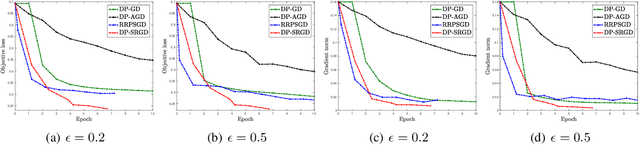
While many solutions for privacy-preserving convex empirical risk minimization (ERM) have been developed, privacy-preserving nonconvex ERM remains under challenging. In this paper, we study nonconvex ERM, which takes the form of minimizing a finite-sum of nonconvex loss functions over a training set. To achieve both efficiency and strong privacy guarantees with efficiency, we propose a differentially-private stochastic gradient descent algorithm for nonconvex ERM, and provide a tight analysis of its privacy and utility guarantees, as well as its gradient complexity. We show that our proposed algorithm can substantially reduce gradient complexity while matching the best-known utility guarantee obtained by Wang et al. (2017). We extend our algorithm to the distributed setting using secure multi-party computation, and show that it is possible for a distributed algorithm to match the privacy and utility guarantees of a centralized algorithm in this setting. Our experiments on benchmark nonconvex ERM problems and real datasets demonstrate superior performance in terms of both training time and utility gains compared with previous differentially-private methods using the same privacy budgets.