Efficient Modeling of Morphing Wing Flight Using Neural Networks and Cubature Rules
Paper and Code
Oct 03, 2021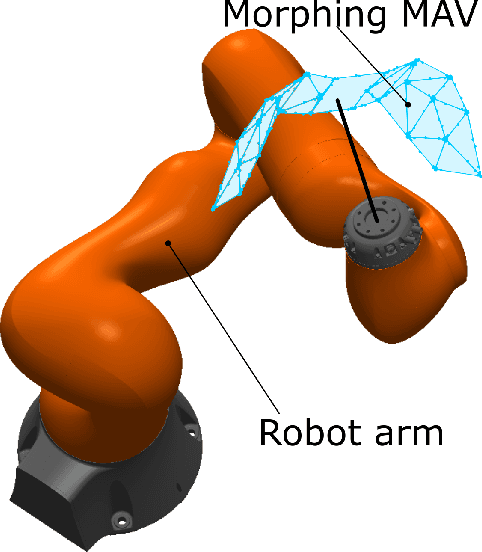
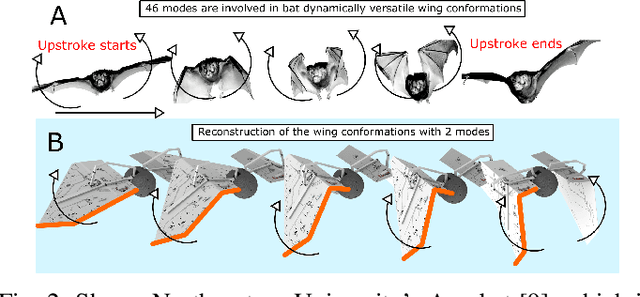
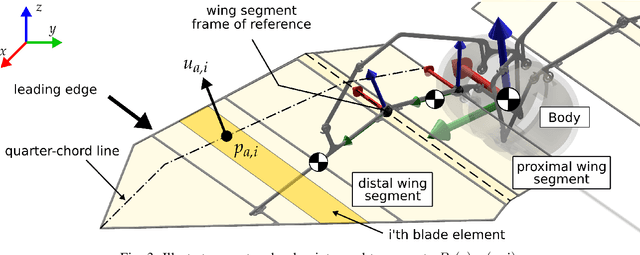
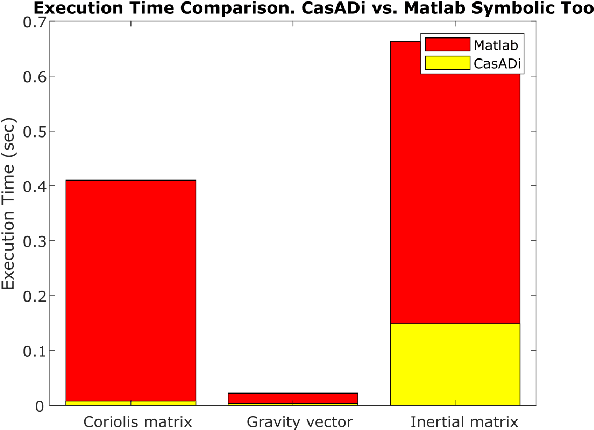
Fluidic locomotion of flapping Micro Aerial Vehicles (MAVs) can be very complex, particularly when the rules from insect flight dynamics (fast flapping dynamics and light wings) are not applicable. In these situations, widely used averaging techniques can fail quickly. The primary motivation is to find efficient models for complex forms of aerial locomotion where wings constitute a large part of body mass (i.e., dominant inertial effects) and deform in multiple directions (i.e., morphing wing). In these systems, high degrees of freedom yields complex inertial, Coriolis, and gravity terms. We use Algorithmic Differentiation (AD) and Bayesian filters computed with cubature rules conjointly to quickly estimate complex fluid-structure interactions. In general, Bayesian filters involve finding complex numerical integration (e.g., find posterior integrals). Using cubature rules to compute Gaussian-weighted integrals and AD, we show that the complex multi-degrees-of-freedom dynamics of morphing MAVs can be computed very efficiently and accurately. Therefore, our work facilitates closed-loop feedback control of these morphing MAVs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge