Efficient Load Sampling for Worst-Case Structural Analysis Under Force Location Uncertainty
Paper and Code
Oct 25, 2018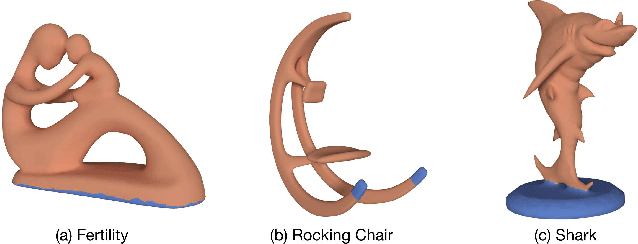
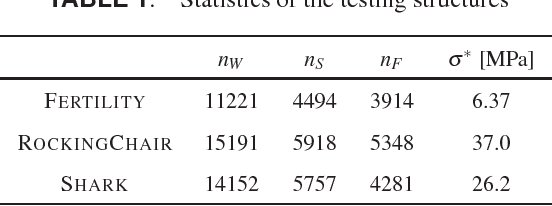
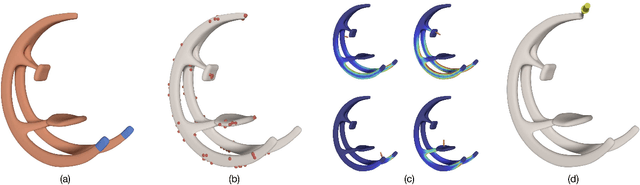
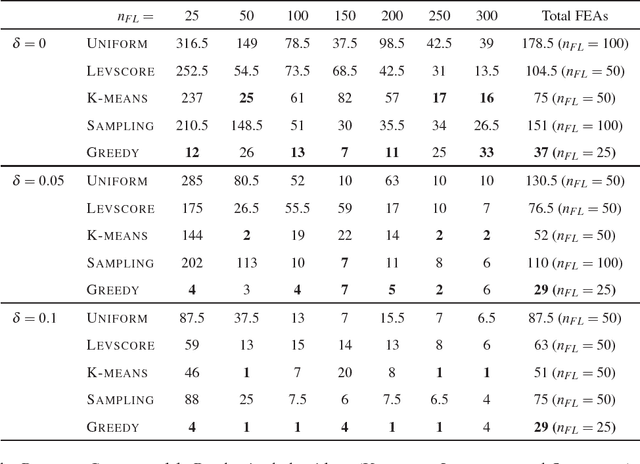
An important task in structural design is to quantify the structural performance of an object under the external forces it may experience during its use. The problem proves to be computationally very challenging as the external forces' contact locations and magnitudes may exhibit significant variations. We present an efficient analysis approach to determine the most critical force contact location in such problems with force location uncertainty. Given an input 3D model and regions on its boundary where arbitrary normal forces may make contact, our algorithm predicts the worst-case force configuration responsible for creating the highest stress within the object. Our approach uses a computationally tractable experimental design method to select number of sample force locations based on geometry only, without inspecting the stress response that requires computationally expensive finite-element analysis. Then, we construct a simple regression model on these samples and corresponding maximum stresses. Combined with a simple ranking based post-processing step, our method provides a practical solution to worst-case structural analysis problem. The results indicate that our approach achieves significant improvements over the existing work and brute force approaches. We demonstrate that further speed- up can be obtained when small amount of an error tolerance in maximum stress is allowed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge