Efficient Distributed Machine Learning via Combinatorial Multi-Armed Bandits
Paper and Code
Feb 16, 2022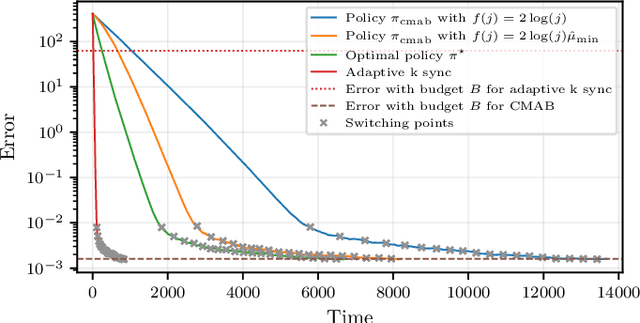
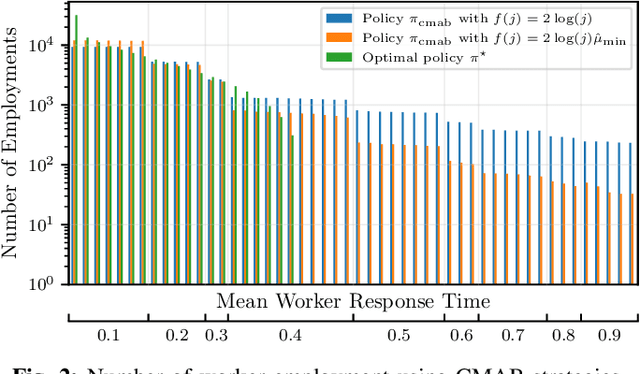
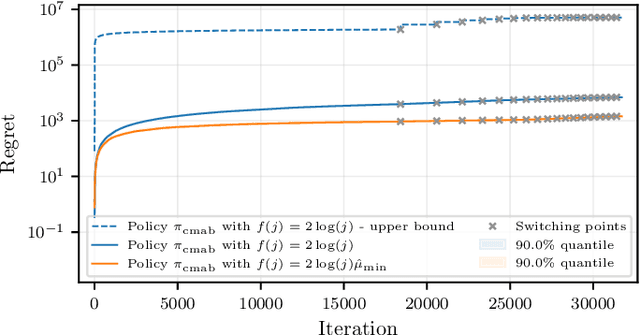
We consider the distributed stochastic gradient descent problem, where a main node distributes gradient calculations among $n$ workers from which at most $b \leq n$ can be utilized in parallel. By assigning tasks to all the workers and waiting only for the $k$ fastest ones, the main node can trade-off the error of the algorithm with its runtime by gradually increasing $k$ as the algorithm evolves. However, this strategy, referred to as adaptive k sync, can incur additional costs since it ignores the computational efforts of slow workers. We propose a cost-efficient scheme that assigns tasks only to $k$ workers and gradually increases $k$. As the response times of the available workers are unknown to the main node a priori, we utilize a combinatorial multi-armed bandit model to learn which workers are the fastest while assigning gradient calculations, and to minimize the effect of slow workers. Assuming that the mean response times of the workers are independent and exponentially distributed with different means, we give empirical and theoretical guarantees on the regret of our strategy, i.e., the extra time spent to learn the mean response times of the workers. Compared to adaptive k sync, our scheme achieves significantly lower errors with the same computational efforts while being inferior in terms of speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge