Efficient Causal Inference from Combined Observational and Interventional Data through Causal Reductions

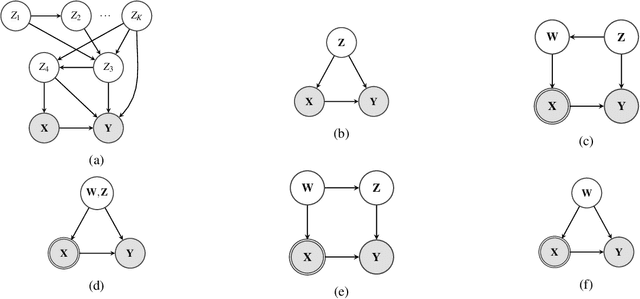
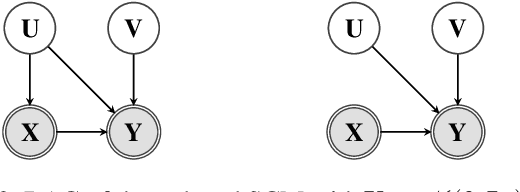
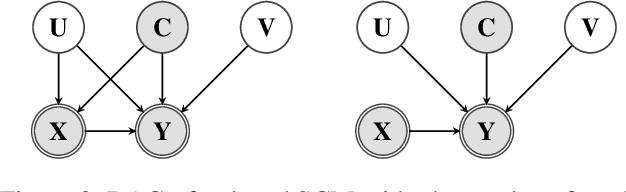
Unobserved confounding is one of the main challenges when estimating causal effects. We propose a novel causal reduction method that replaces an arbitrary number of possibly high-dimensional latent confounders with a single latent confounder that lives in the same space as the treatment variable without changing the observational and interventional distributions entailed by the causal model. After the reduction, we parameterize the reduced causal model using a flexible class of transformations, so-called normalizing flows. We propose a learning algorithm to estimate the parameterized reduced model jointly from observational and interventional data. This allows us to estimate the causal effect in a principled way from combined data. We perform a series of experiments on data simulated using nonlinear causal mechanisms and find that we can often substantially reduce the number of interventional samples when adding observational training samples without sacrificing accuracy. Thus, adding observational data may help to more accurately estimate causal effects even in the presence of unobserved confounders.