Efficient Arbitrary Precision Acceleration for Large Language Models on GPU Tensor Cores

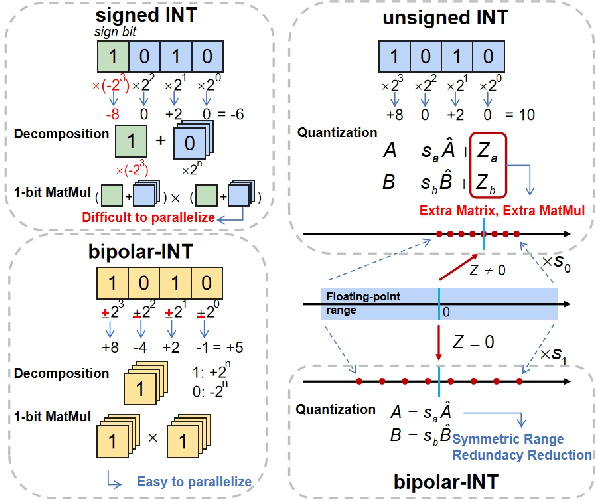
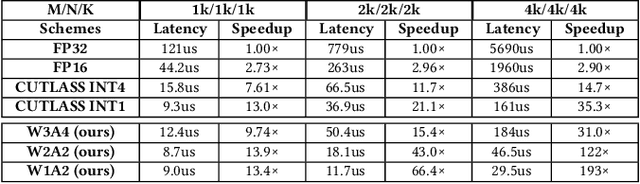
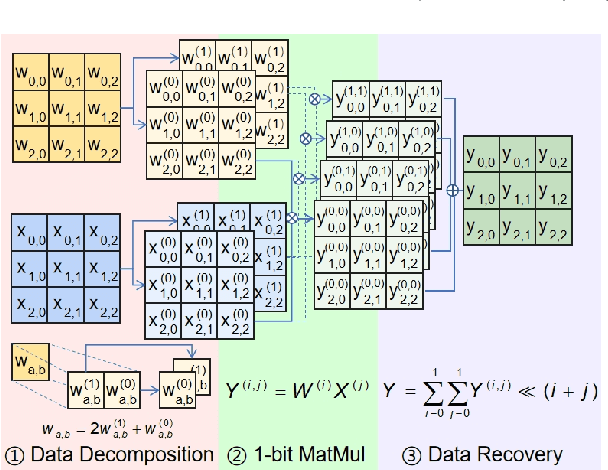
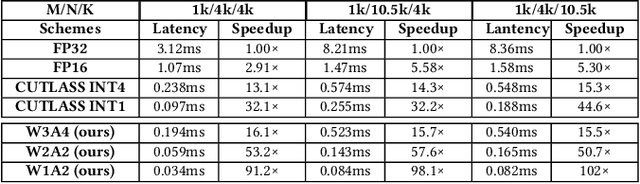
Large language models (LLMs) have been widely applied but face challenges in efficient inference. While quantization methods reduce computational demands, ultra-low bit quantization with arbitrary precision is hindered by limited GPU Tensor Core support and inefficient memory management, leading to suboptimal acceleration. To address these challenges, we propose a comprehensive acceleration scheme for arbitrary precision LLMs. At its core, we introduce a novel bipolar-INT data format that facilitates parallel computing and supports symmetric quantization, effectively reducing data redundancy. Building on this, we implement an arbitrary precision matrix multiplication scheme that decomposes and recovers matrices at the bit level, enabling flexible precision while maximizing GPU Tensor Core utilization. Furthermore, we develop an efficient matrix preprocessing method that optimizes data layout for subsequent computations. Finally, we design a data recovery-oriented memory management system that strategically utilizes fast shared memory, significantly enhancing kernel execution speed and minimizing memory access latency. Experimental results demonstrate our approach's effectiveness, with up to 13\times speedup in matrix multiplication compared to NVIDIA's CUTLASS. When integrated into LLMs, we achieve up to 6.7\times inference acceleration. These improvements significantly enhance LLM inference efficiency, enabling broader and more responsive applications of LLMs.