Efficient and Consistent Bundle Adjustment on Lidar Point Clouds
Paper and Code
Sep 19, 2022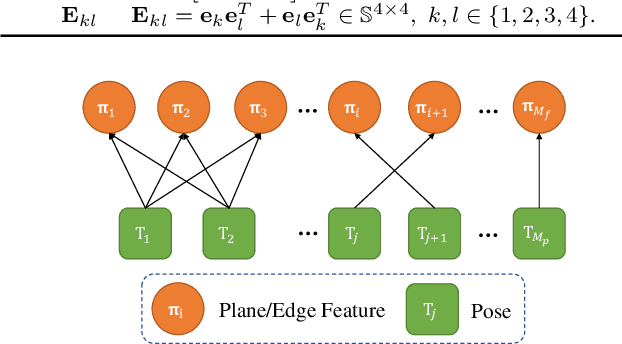
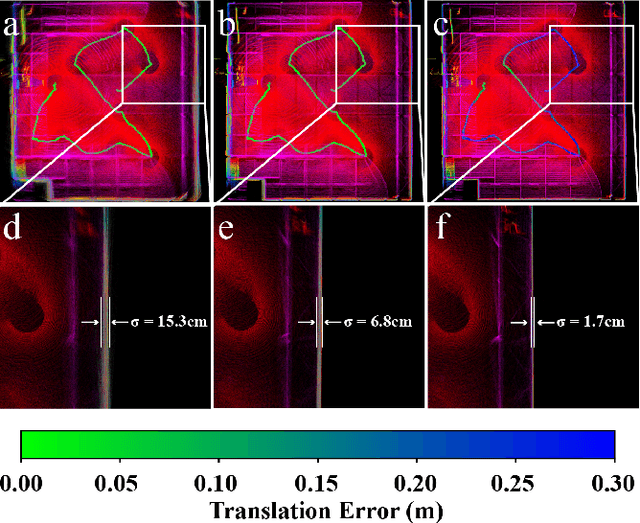
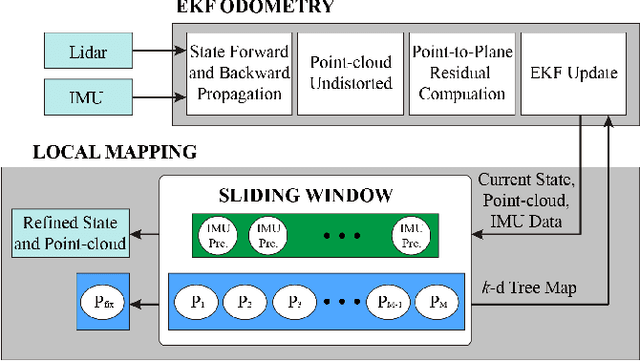
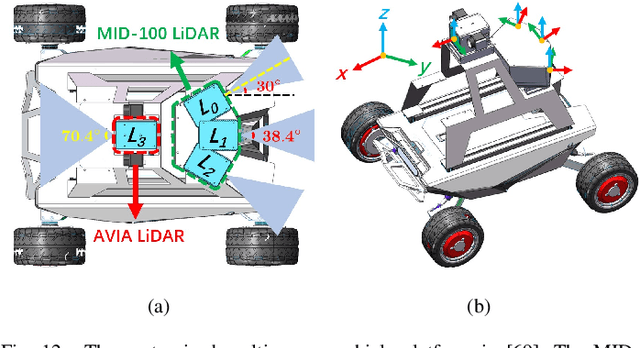
Bundle Adjustment (BA) refers to the problem of simultaneous determination of sensor poses and scene geometry, which is a fundamental problem in robot vision. This paper presents an efficient and consistent bundle adjustment method for lidar sensors. The method employs edge and plane features to represent the scene geometry, and directly minimizes the natural Euclidean distance from each raw point to the respective geometry feature. A nice property of this formulation is that the geometry features can be analytically solved, drastically reducing the dimension of the numerical optimization. To represent and solve the resultant optimization problem more efficiently, this paper then proposes a novel concept {\it point clusters}, which encodes all raw points associated to the same feature by a compact set of parameters, the {\it point cluster coordinates}. We derive the closed-form derivatives, up to the second order, of the BA optimization based on the point cluster coordinates and show their theoretical properties such as the null spaces and sparsity. Based on these theoretical results, this paper develops an efficient second-order BA solver. Besides estimating the lidar poses, the solver also exploits the second order information to estimate the pose uncertainty caused by measurement noises, leading to consistent estimates of lidar poses. Moreover, thanks to the use of point cluster, the developed solver fundamentally avoids the enumeration of each raw point (which is very time-consuming due to the large number) in all steps of the optimization: cost evaluation, derivatives evaluation and uncertainty evaluation. The implementation of our method is open sourced to benefit the robotics community and beyond.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge