Efficient-Adam: Communication-Efficient Distributed Adam with Complexity Analysis
Paper and Code
May 28, 2022

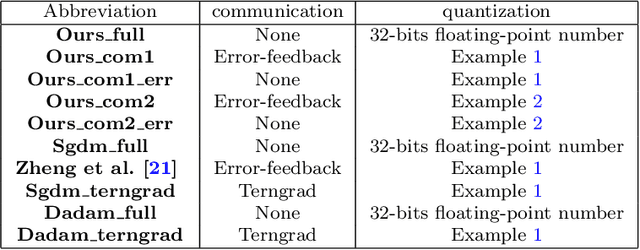

Distributed adaptive stochastic gradient methods have been widely used for large-scale nonconvex optimization, such as training deep learning models. However, their communication complexity on finding $\varepsilon$-stationary points has rarely been analyzed in the nonconvex setting. In this work, we present a novel communication-efficient distributed Adam in the parameter-server model for stochastic nonconvex optimization, dubbed {\em Efficient-Adam}. Specifically, we incorporate a two-way quantization scheme into Efficient-Adam to reduce the communication cost between the workers and server. Simultaneously, we adopt a two-way error feedback strategy to reduce the biases caused by the two-way quantization on both the server and workers, respectively. In addition, we establish the iteration complexity for the proposed Efficient-Adam with a class of quantization operators, and further characterize its communication complexity between the server and workers when an $\varepsilon$-stationary point is achieved. Finally, we apply Efficient-Adam to solve a toy stochastic convex optimization problem and train deep learning models on real-world vision and language tasks. Extensive experiments together with a theoretical guarantee justify the merits of Efficient Adam.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge