DWMD: Dimensional Weighted Orderwise Moment Discrepancy for Domain-specific Hidden Representation Matching

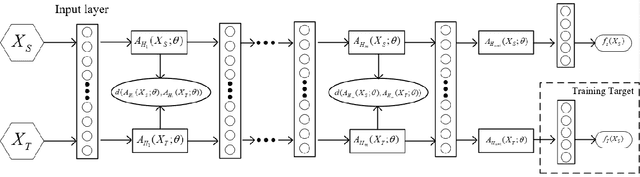
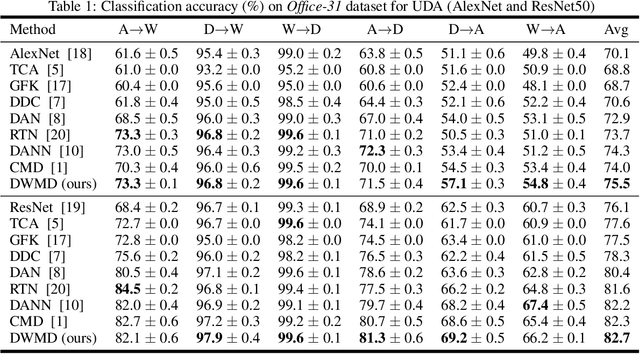
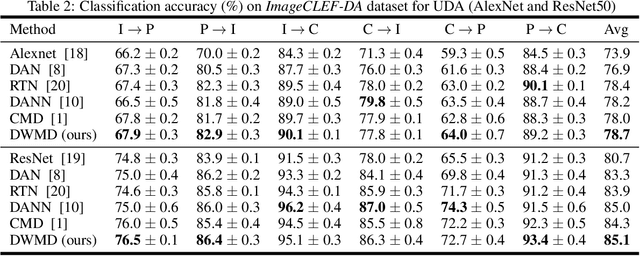
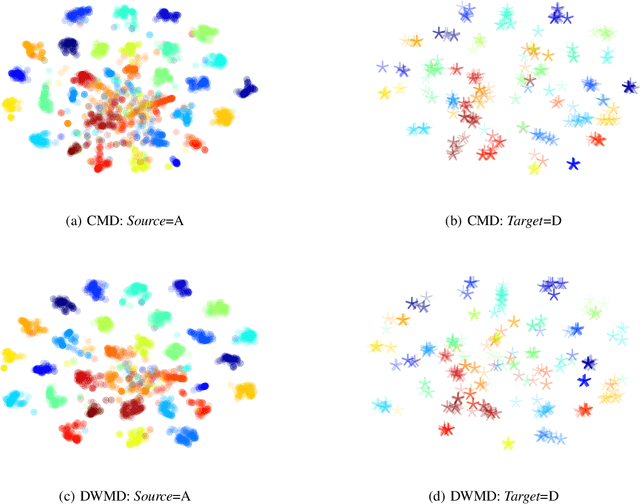
Knowledge transfer from a source domain to a different but semantically related target domain has long been an important topic in the context of unsupervised domain adaptation (UDA). A key challenge in this field is establishing a metric that can exactly measure the data distribution discrepancy between two homogeneous domains and adopt it in distribution alignment, especially in the matching of feature representations in the hidden activation space. Existing distribution matching approaches can be interpreted as failing to either explicitly orderwise align higher-order moments or satisfy the prerequisite of certain assumptions in practical uses. We propose a novel moment-based probability distribution metric termed dimensional weighted orderwise moment discrepancy (DWMD) for feature representation matching in the UDA scenario. Our metric function takes advantage of a series for high-order moment alignment, and we theoretically prove that our DWMD metric function is error-free, which means that it can strictly reflect the distribution differences between domains and is valid without any feature distribution assumption. In addition, since the discrepancies between probability distributions in each feature dimension are different, dimensional weighting is considered in our function. We further calculate the error bound of the empirical estimate of the DWMD metric in practical applications. Comprehensive experiments on benchmark datasets illustrate that our method yields state-of-the-art distribution metrics.